Overview

Like the first project, actually implementing functions helped me better appreciate why we use data structures like half edges for operations like mesh traversal and transforms when it may at first seem simpler to use sets of vertices and edges. I also gained a better intuition behind algorithms like loop subdivision by implementing the different steps myself and having to think about how and when to keep track of values like the transformed positions. With all the pointers used to represent meshes with the halfedge data structure, this project was definitely harder to debug than the first project.

Section I: Bezier Curves and Surfaces

Part 1: Bezier curves with 1D de Casteljau subdivision

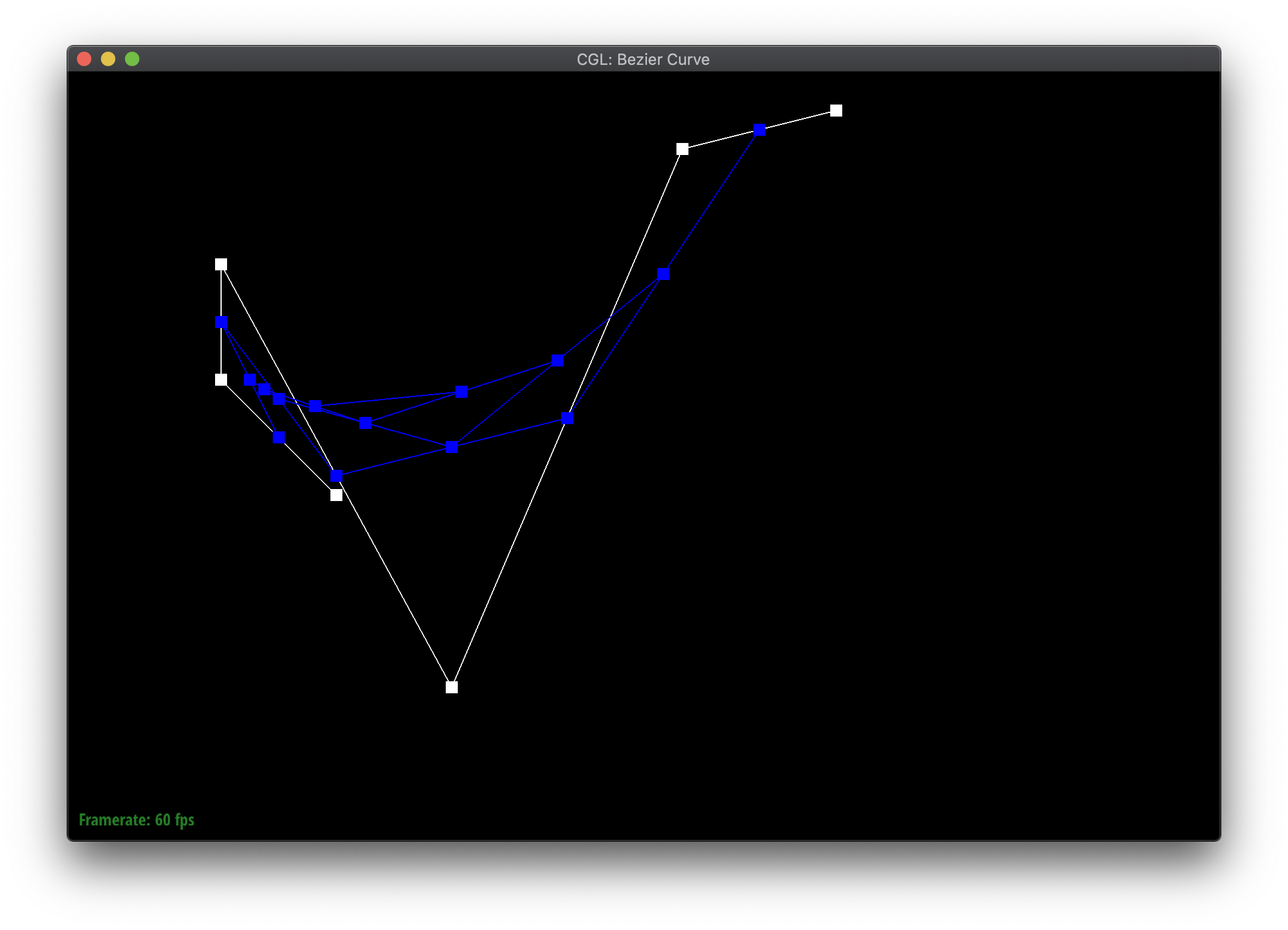
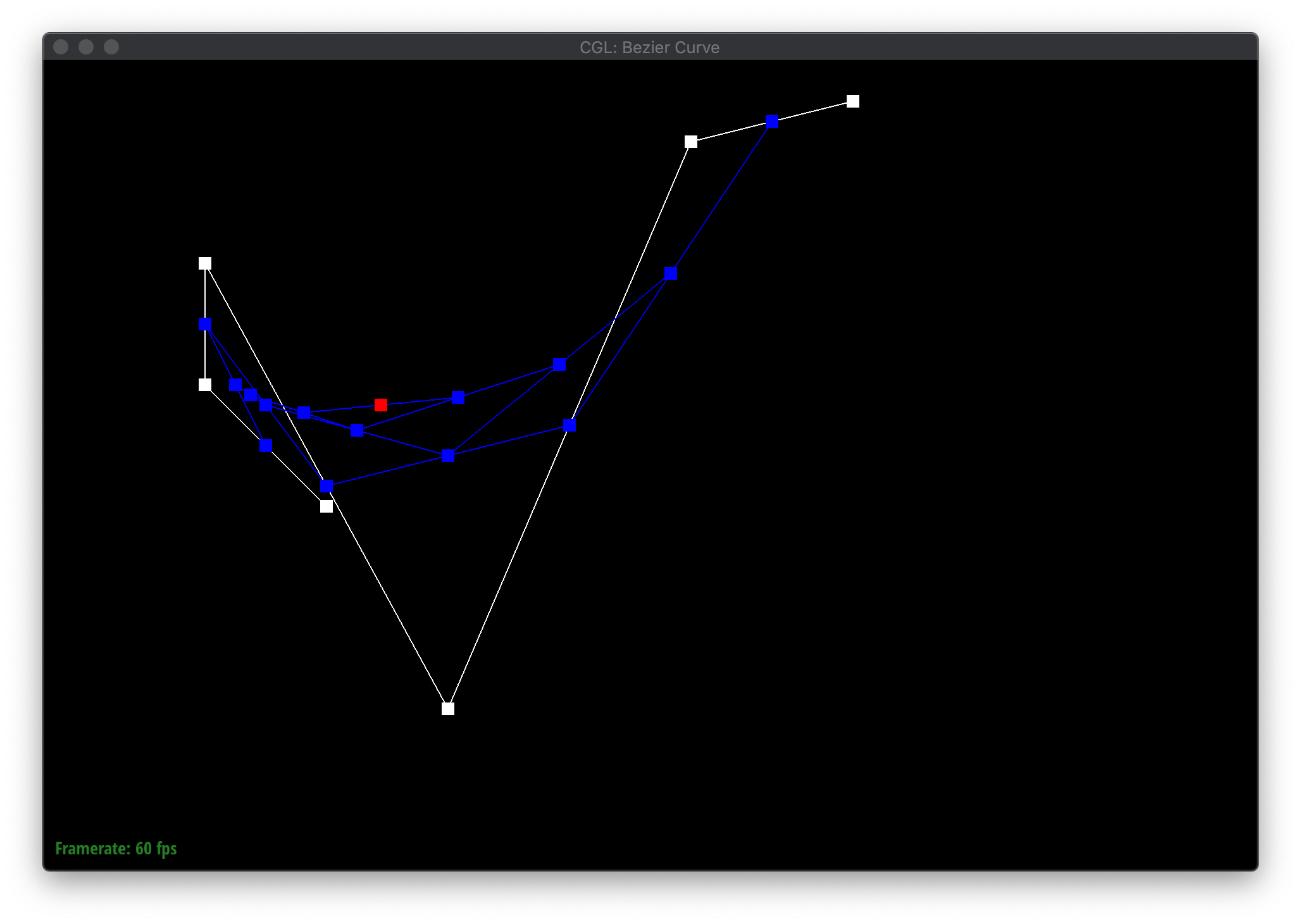
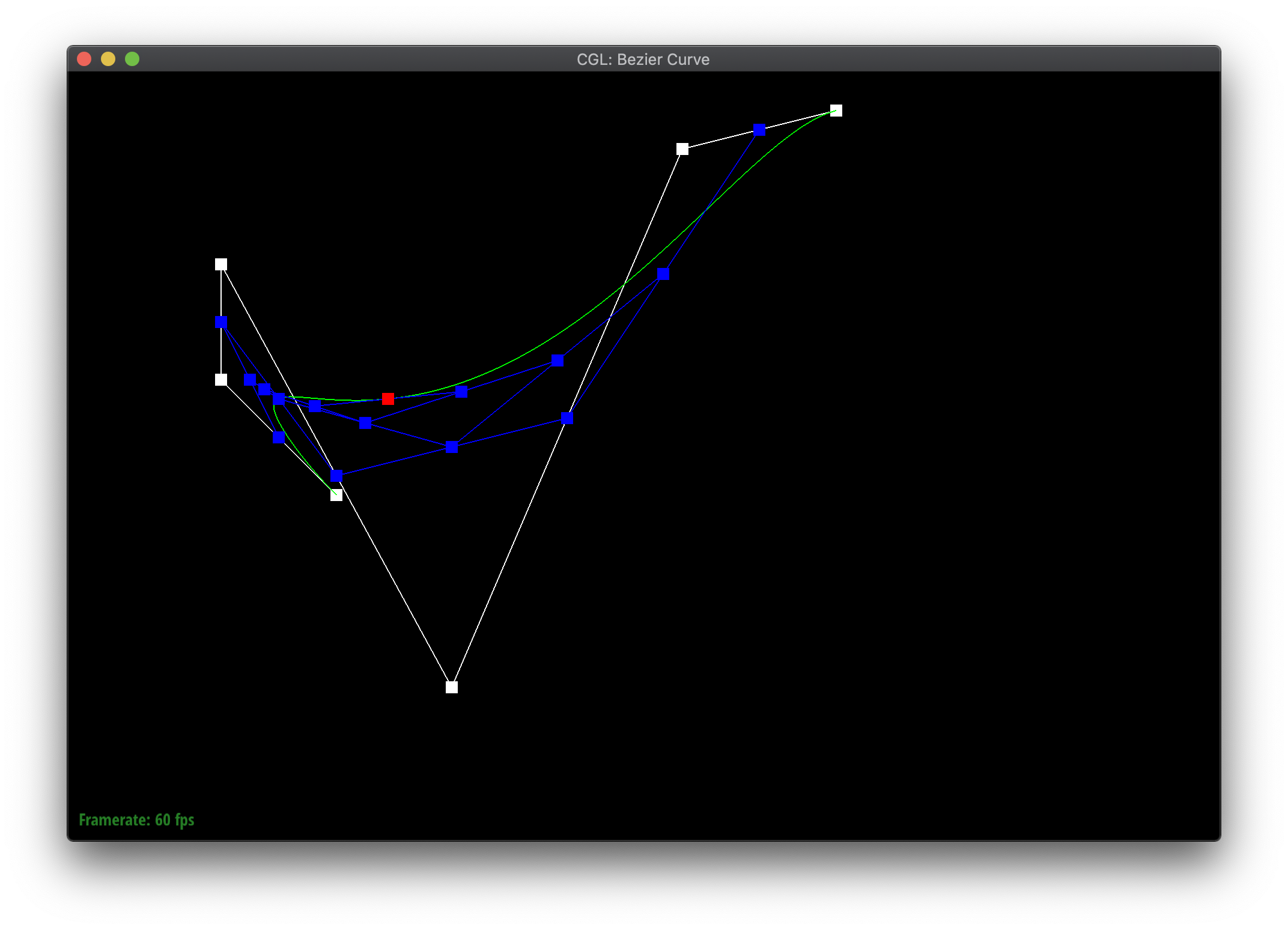
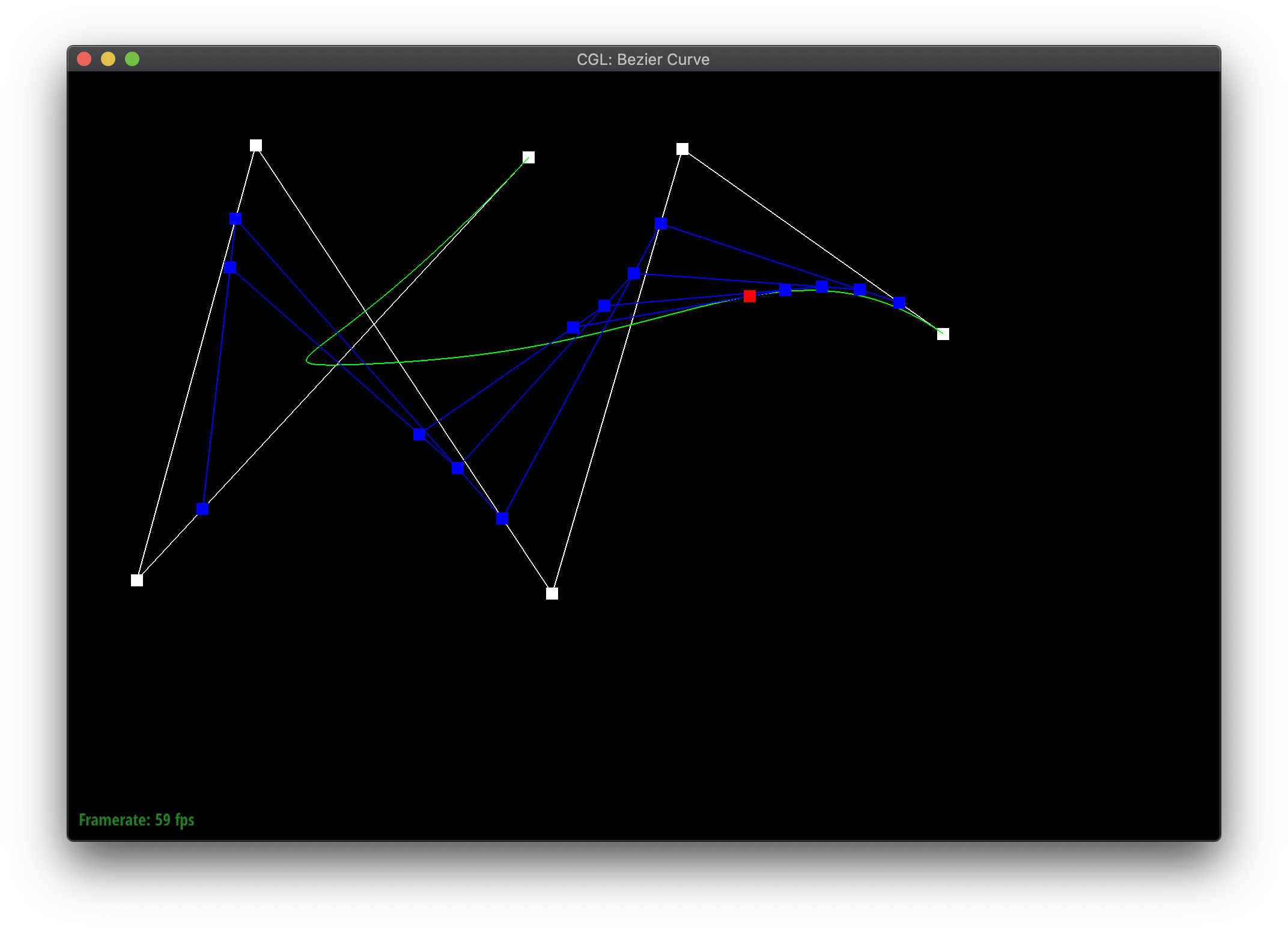
Bezier curves are defined by a series of control points. The de Casteljau algorithm iteratively or recursively defines how to evaluate the curve based on the points. Given a parameter \(t\) between 0 and 1, the point for the next level is \(t\) proportionally along a line connecting each pair of consecutive points, effectively reducing the number of points by one each time. More specifically, given 2 points \((x_1, y_1\) and \((x_2, y_2\), the next point is \(((1-t) * x_1 + t * x_2, (1-t) * y_1 + t * y_2) \). The algorithm terminates when there is only a single point remaining, which is a point on the Bezier curve.

The blue points are the result of evaluating each iteration of de Casteljau's algorithm on the white control points. The red point in the last step is a point on the resulting Bezier curve.

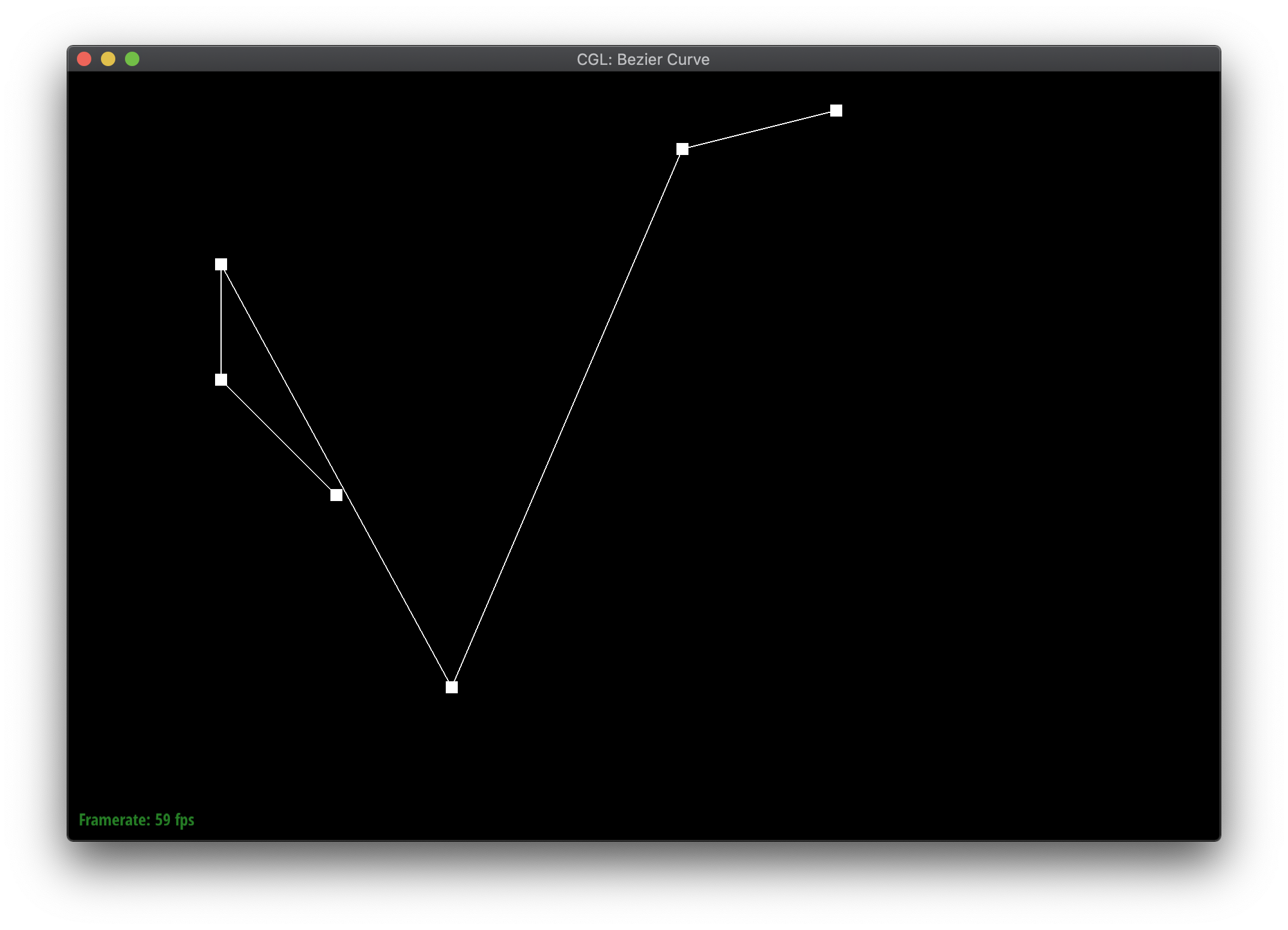
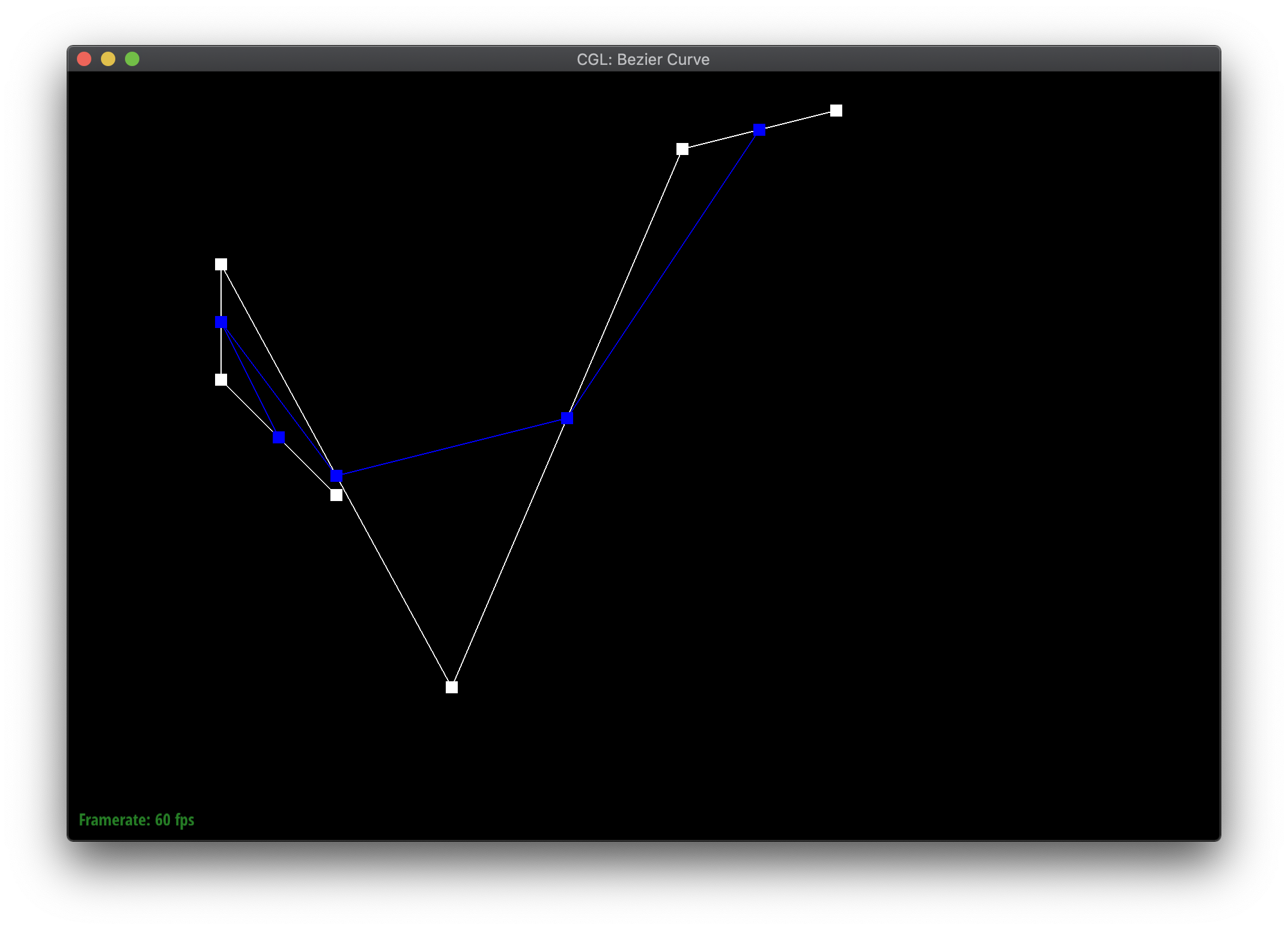
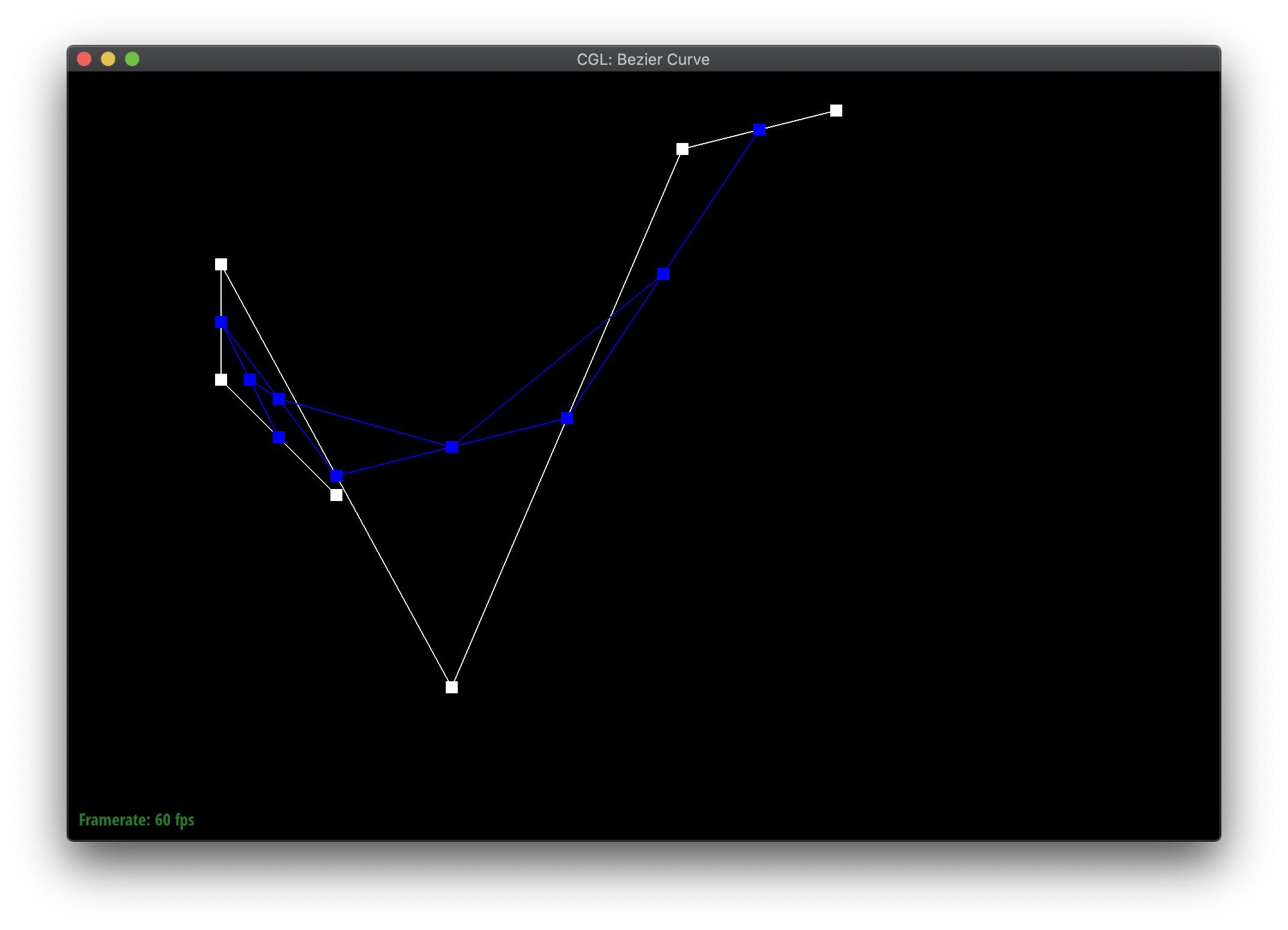
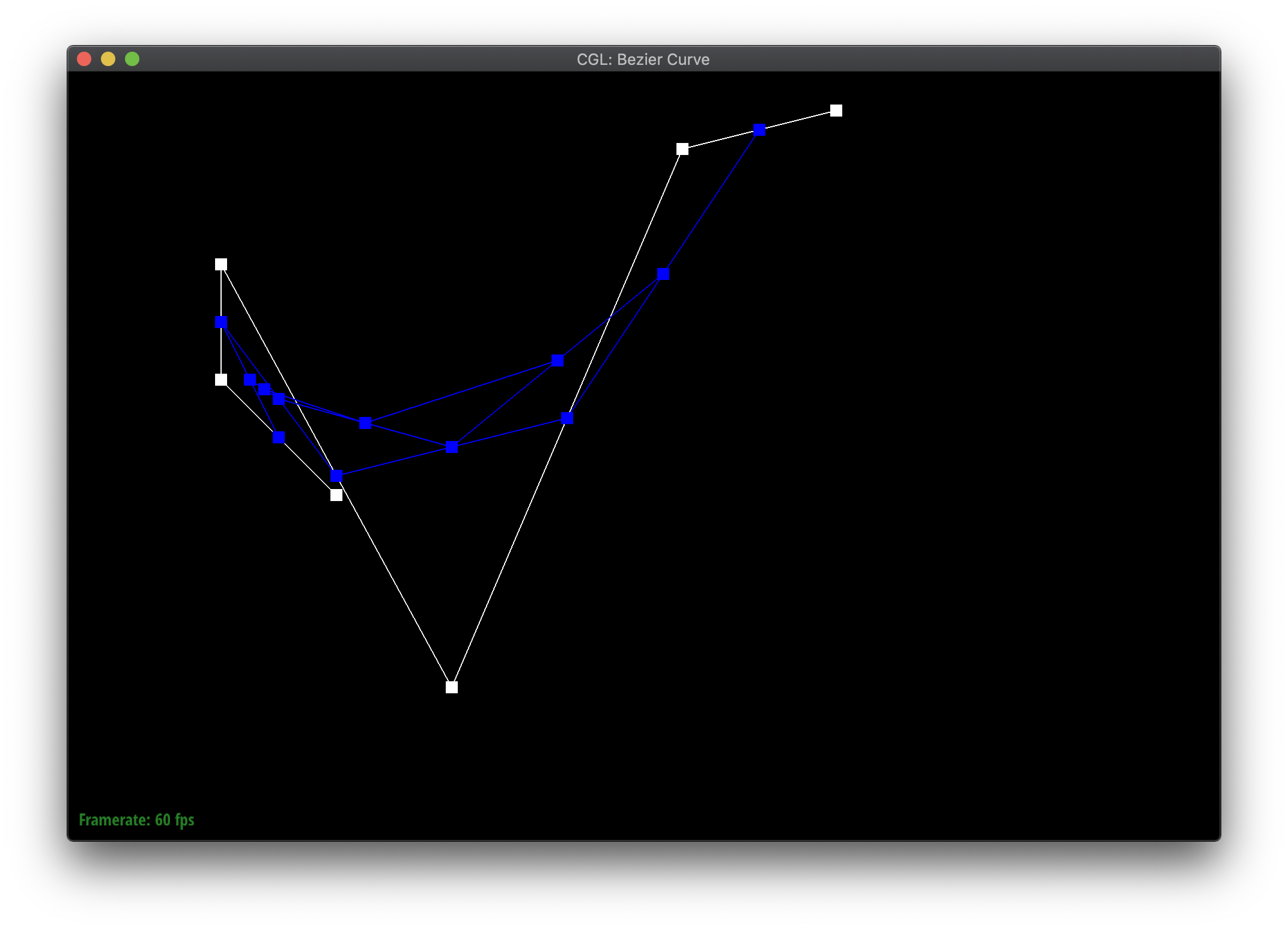
Part 2: Bezier surfaces with separable 1D de Casteljau subdivision

Expanding from 2D Bezier curves to 3D surfaces, we still use the basic de Casteljau algorithm. Given an \(n \times n\) grid of control points and parametric parameters \(u\) and \(v\), we first evaluate the Bezier curves created in by the points in each row (reducing each row to a single point) with parameter \(u\). Each of those single points are then the control points for a Bezier curve that can be evaluated with parameter \(v\), resulting in a point on the Bezier surface evaluated at \(u\) and \(v\).

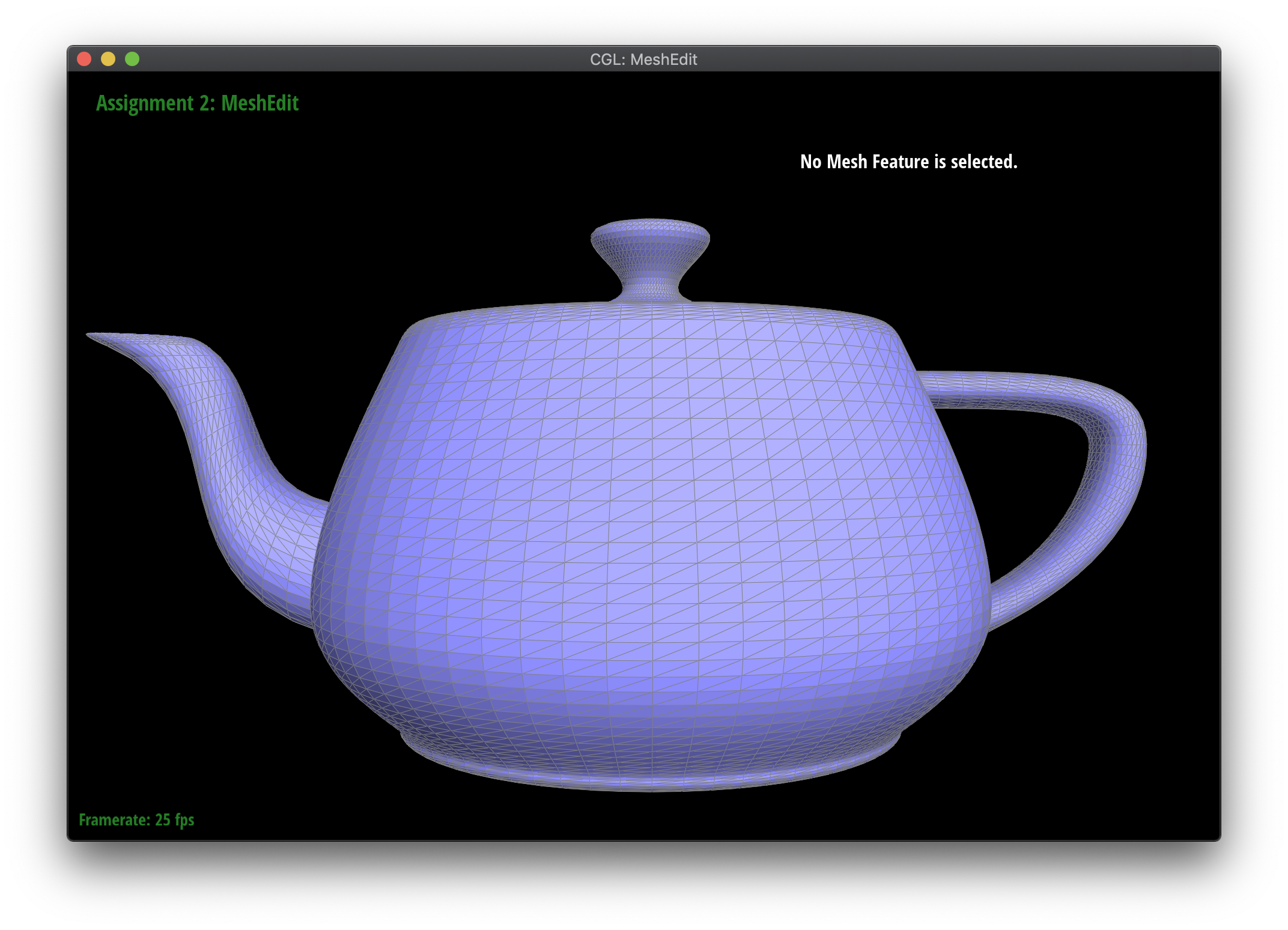
Section II: Sampling

Part 3: Average normals for halfedge meshes

In this part, I implemented area weighted normals for each vertex. Iterating through the faces of a vertex via half edges (given a starting half edge, the next triangle would be that half edge's twin's next), for each face I found the coordinates of the 3 vertices and used those to compute the face area. I kept a running total normal vector and for each face added its normal vector, weighted by the face area. Finally, I normalized the normal vector.

Phong shading produces much smoother changes along the surface than flat shading.

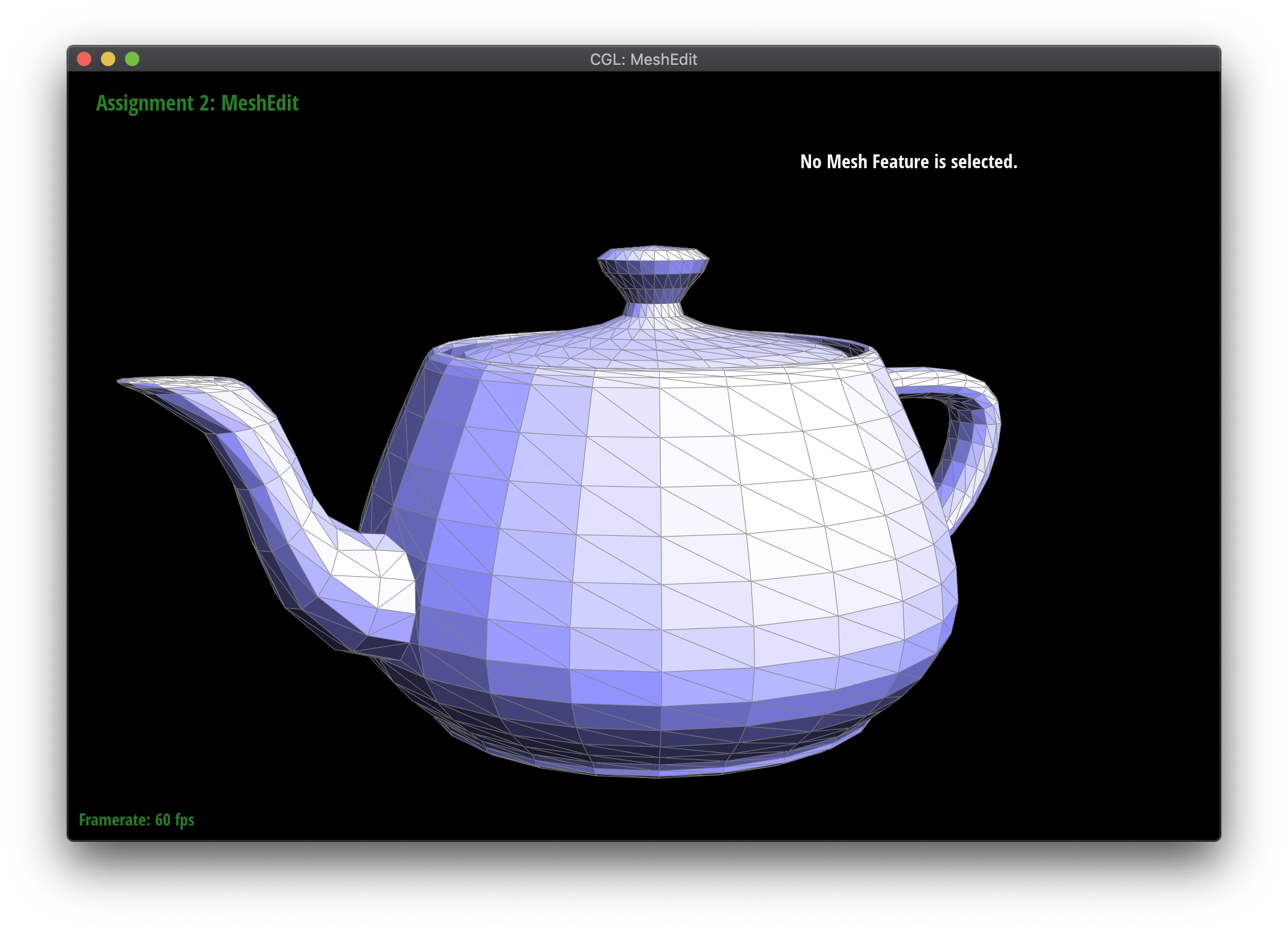
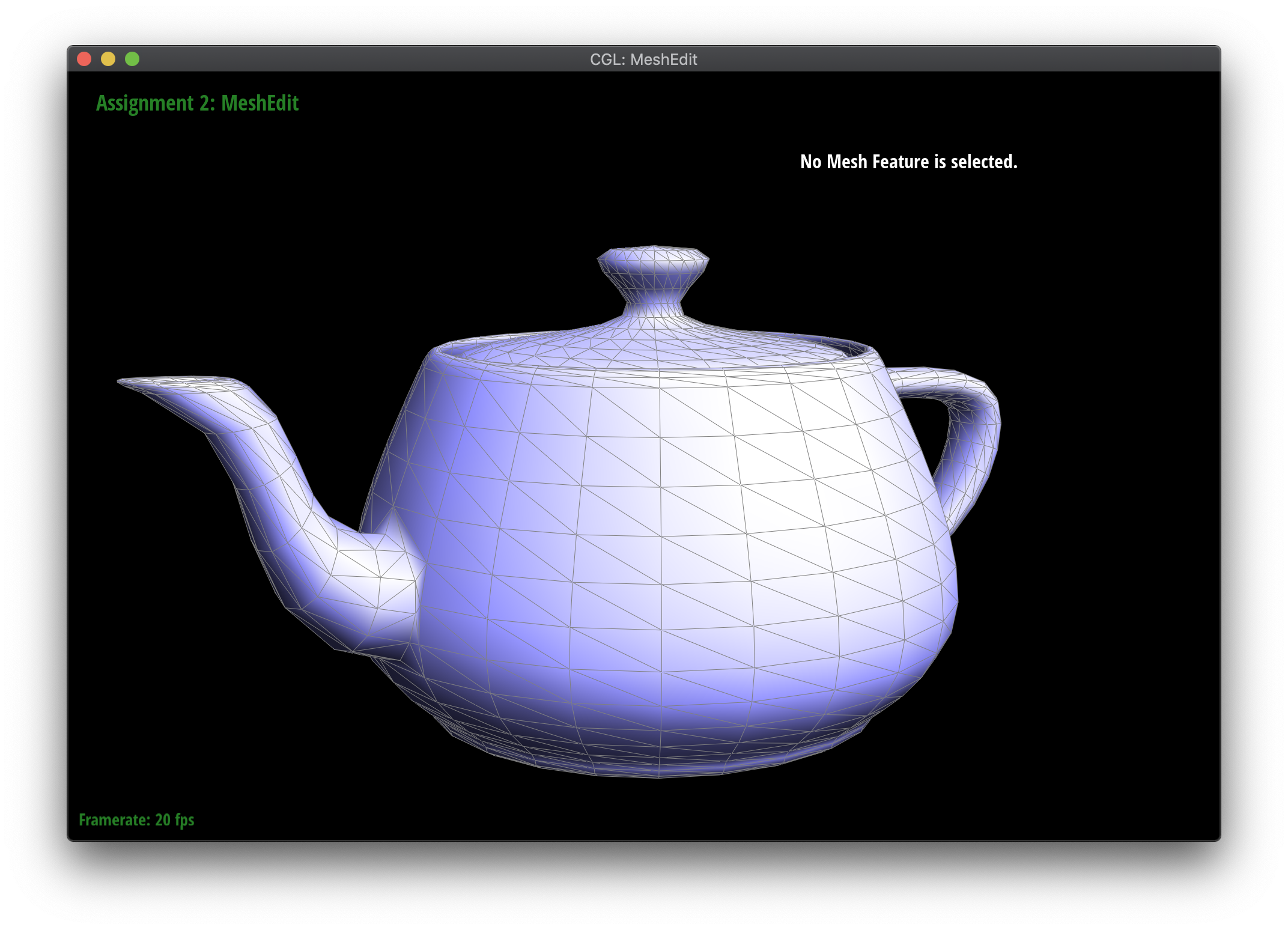
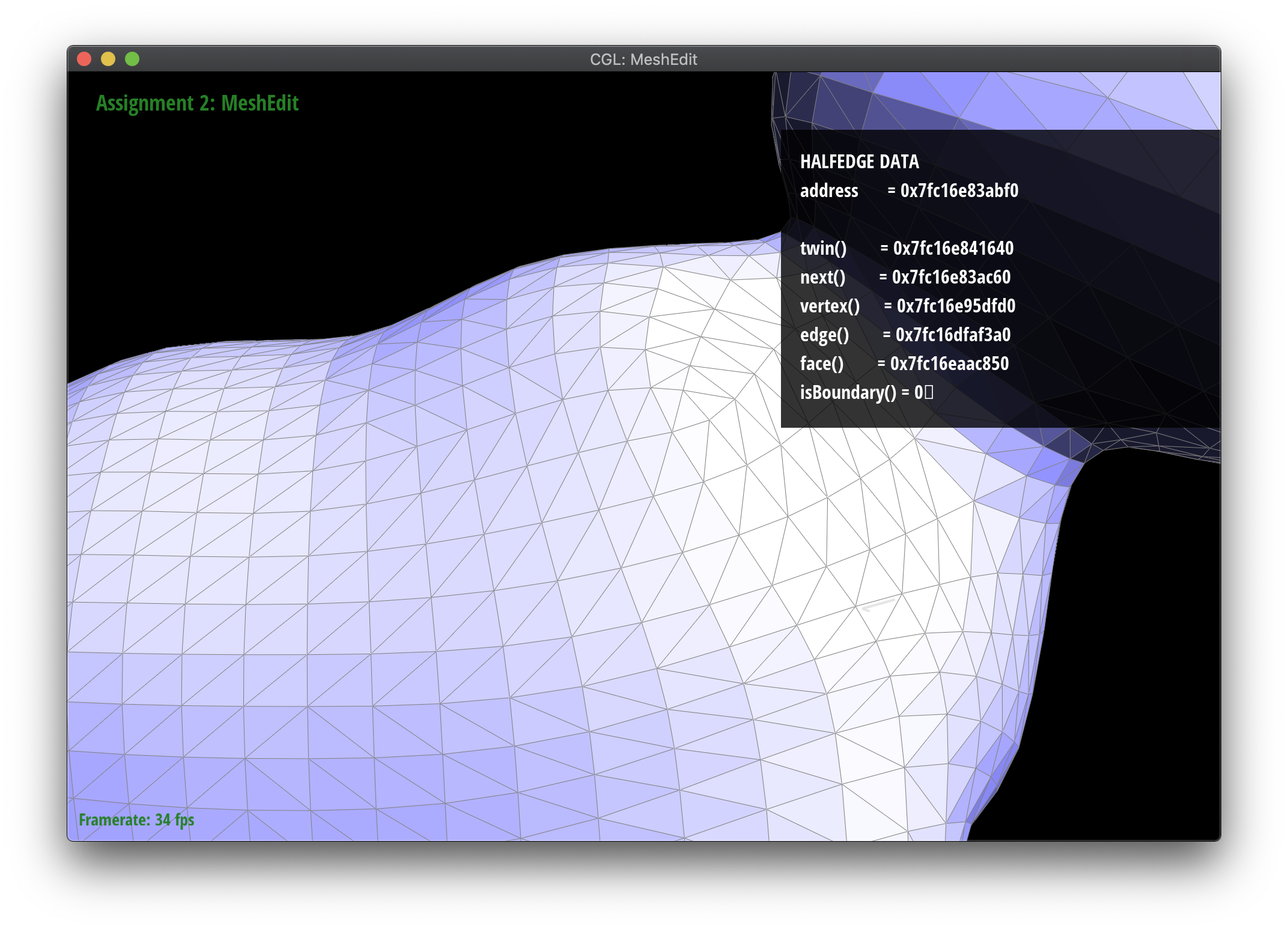
Part 4: Halfedge flip

In order to keep track of all the halfedges, edges, vertices, and faces, I wrote down each one and their relationships before and after flipping, using the above diagram as a guide. Flipping does not require any actual addition or deletion of halfedges, only renaming (for example \(bc\) becomes \(ad\) ) which is just pointer manipulation. In implementing this section, I first found all the pointers to the relevant mesh elements, renamed them if necessary, and reassigned their contained pointers (halfedges for faces, vertices, and edges and next halfedge, twin halfedge, vertex, edge, and face for halfedges) to their appropriate new ones.

Part 5: Halfedge split

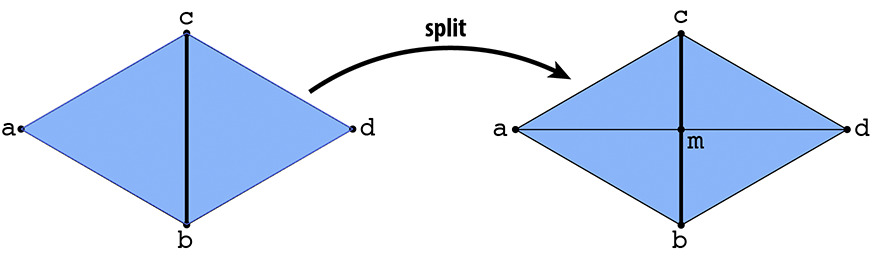
Unlike the edge flip operation, the edge split operation, which consists of splitting a given edge in half, creating 4 triangles from an original single one, requires creating new mesh elements: 1 midpoint vertex, 2 new faces, 3 new edges, and 6 new halfedges. In implementing this part, I wrote down all the elements and their relationships for the diagram above both before and after the split to keep track of everything. Then I found all the pointers to the elements from the given input edges, created the necessary new elements, and assigned the correct pointers to match the right side of the diagram above.

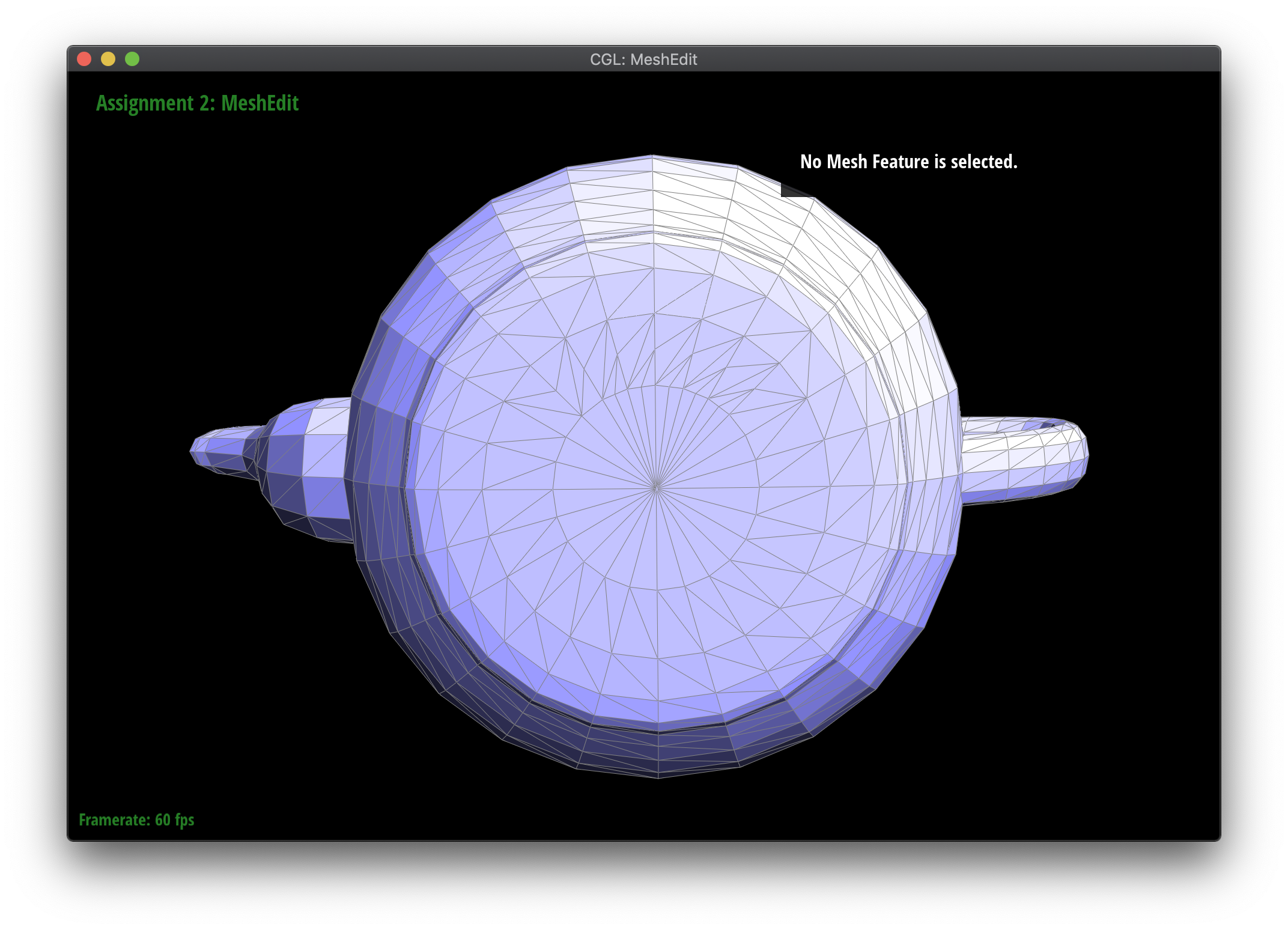
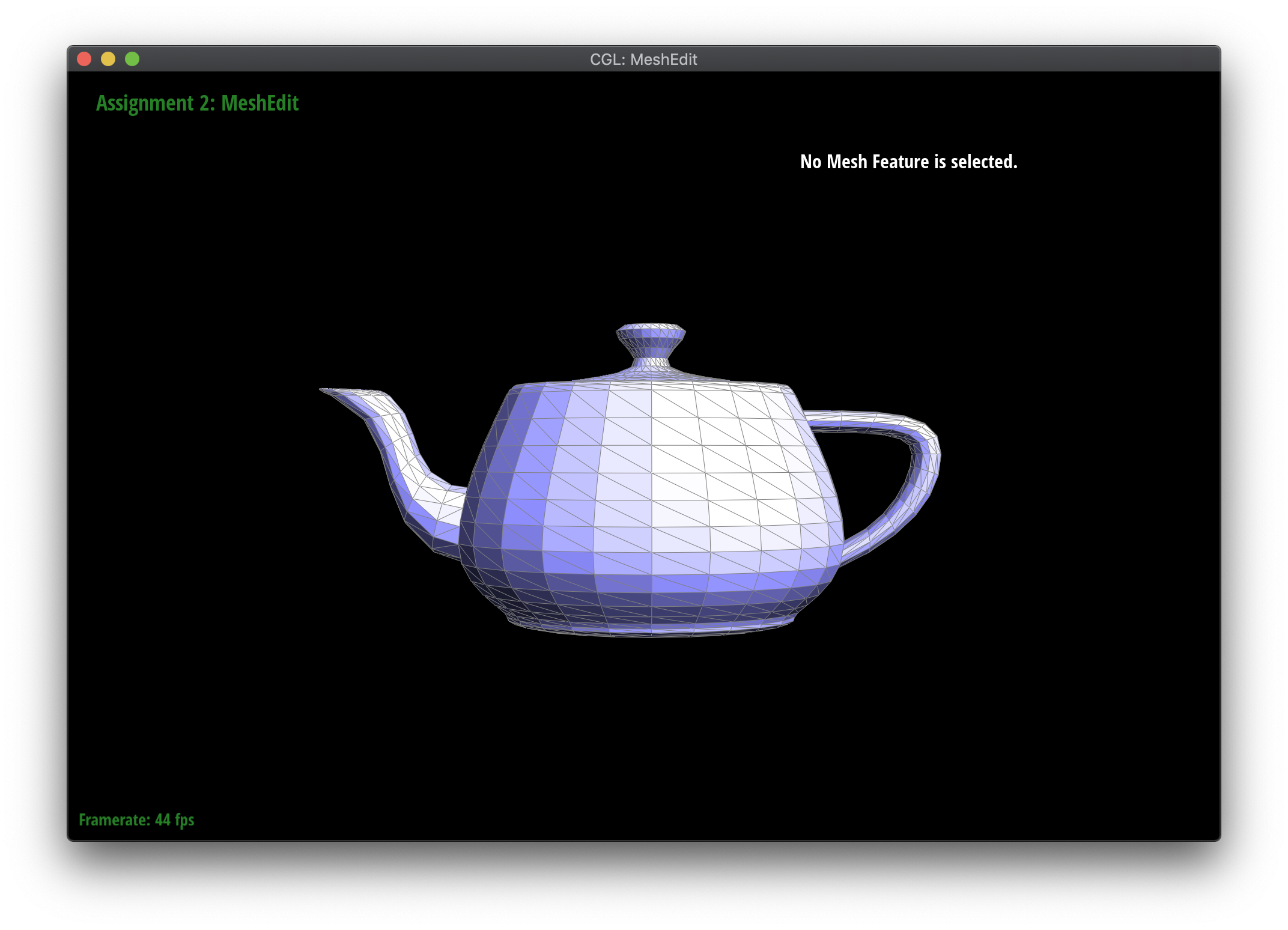
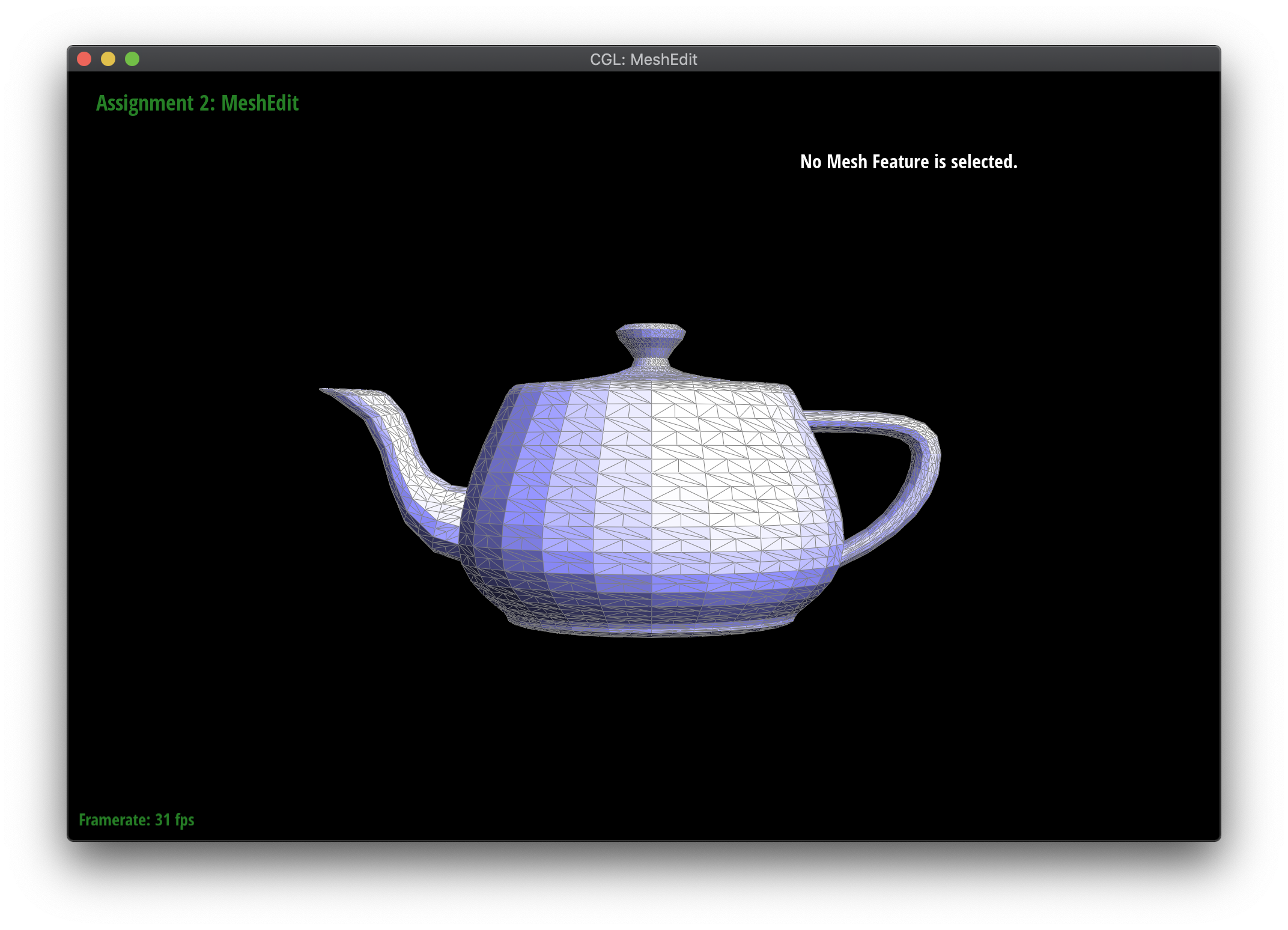
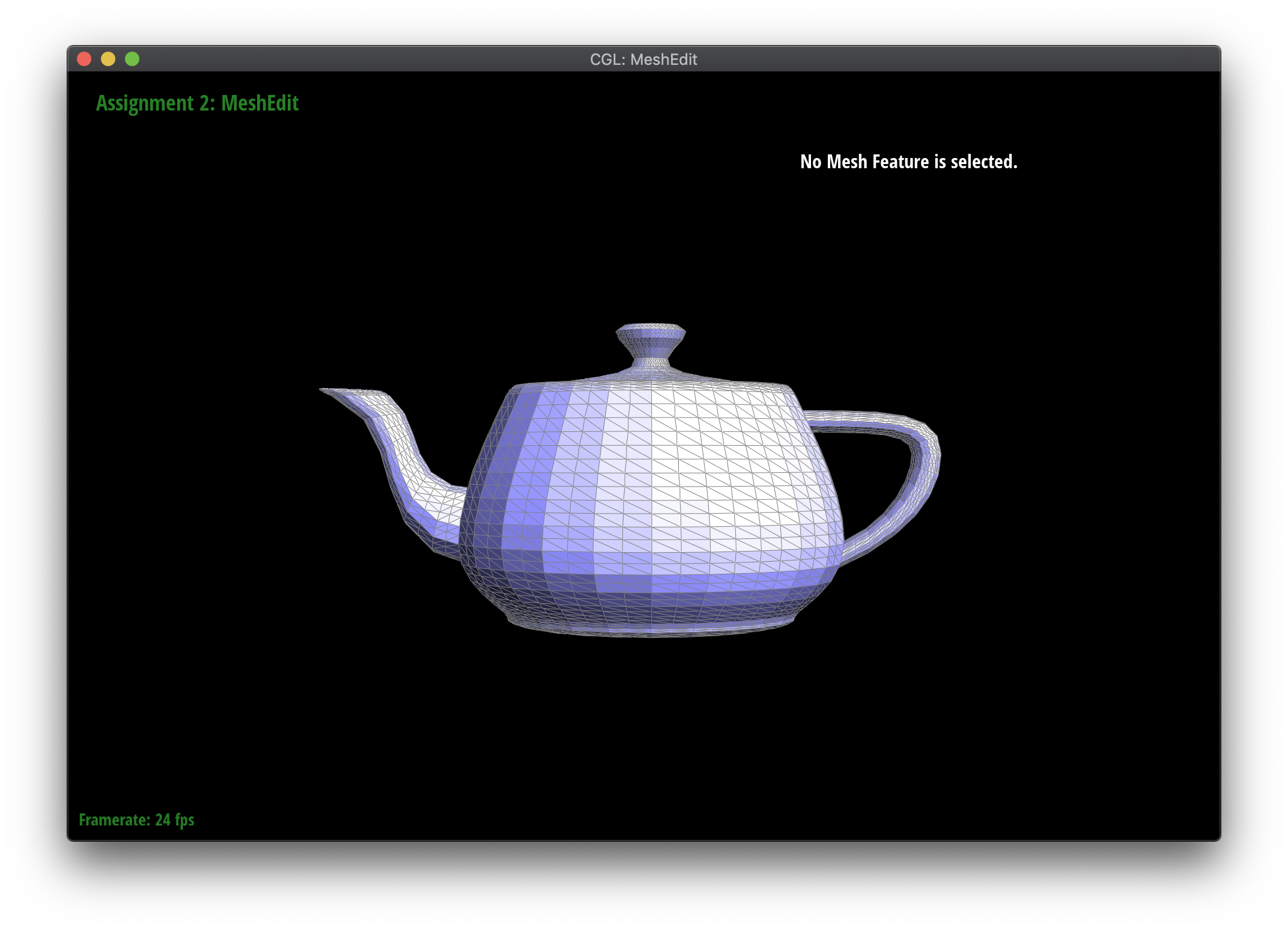
Part 6: Loop subdivision for mesh upsampling

In this part, I implemented the loop subdivision algorithm, used to upsample the mesh by creating new vertices and edges using the halfedge flip and split methods written above. Each edge in the original mesh is split, and edges between new and old vertices are flipped to create more uniform triangles, as shown in the above diagram. Lastly, both new and old vertex positions are reweighted based on the position of neighboring vertices.

Because vertex positions are reweighted based on positions in the original mesh, I used the newPosition attribute in the Vertex (for existing mesh vertices) and Edge (for the new vertex to be created on an edge) classes to keep track of what the new position would be. This required careful modification of the halfedge flip method from before to make sure newPosition remained properly set.

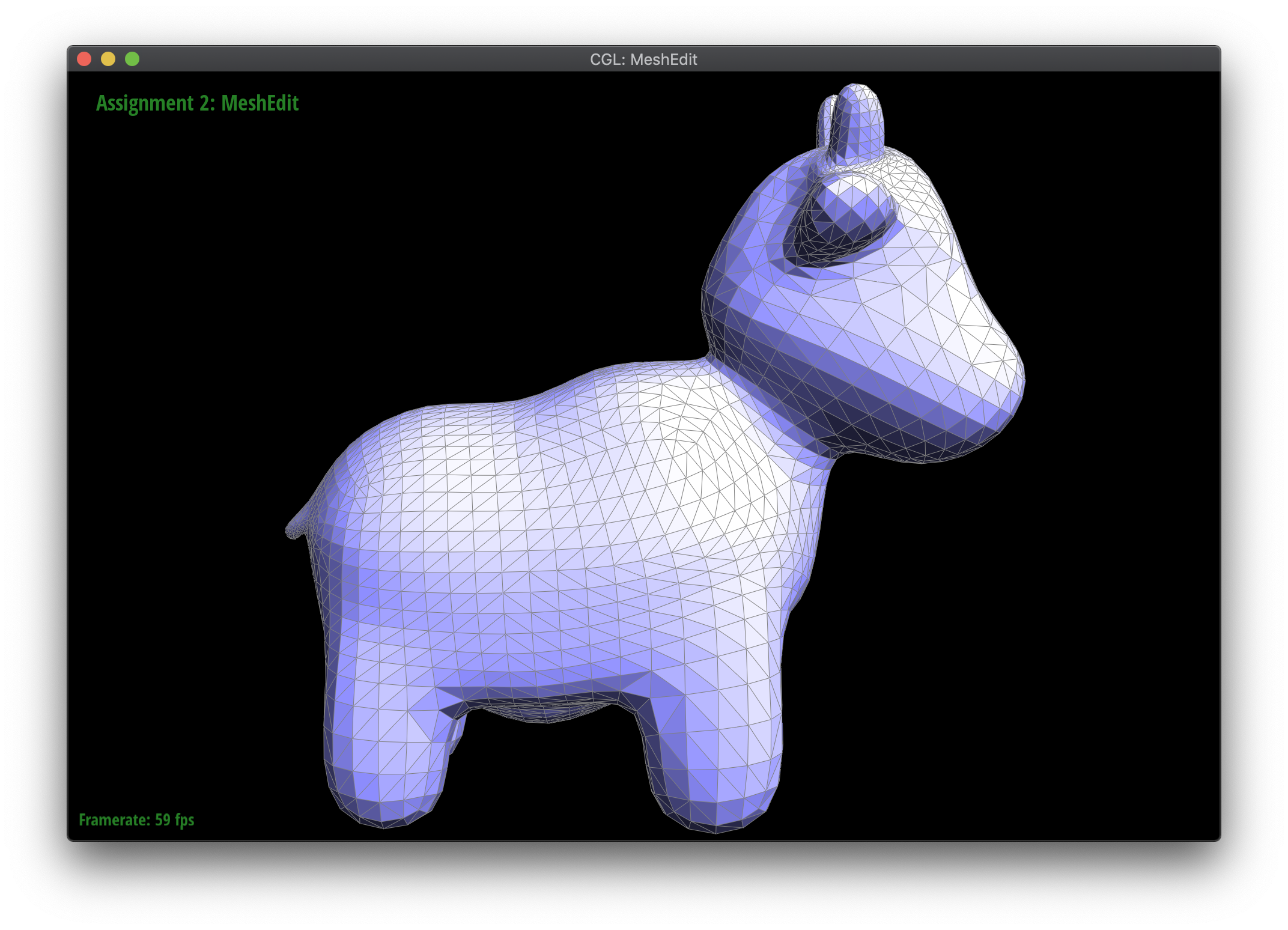
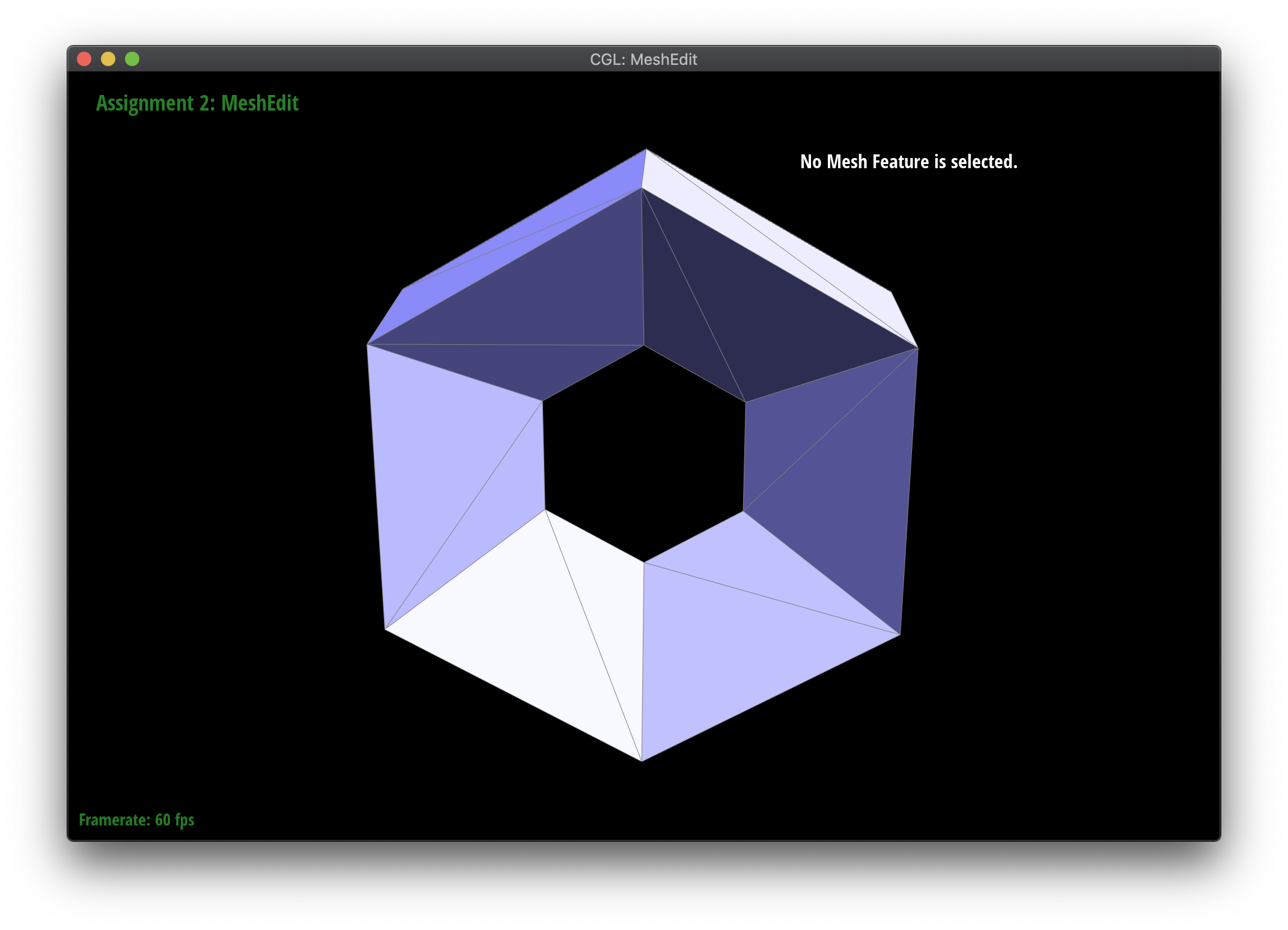
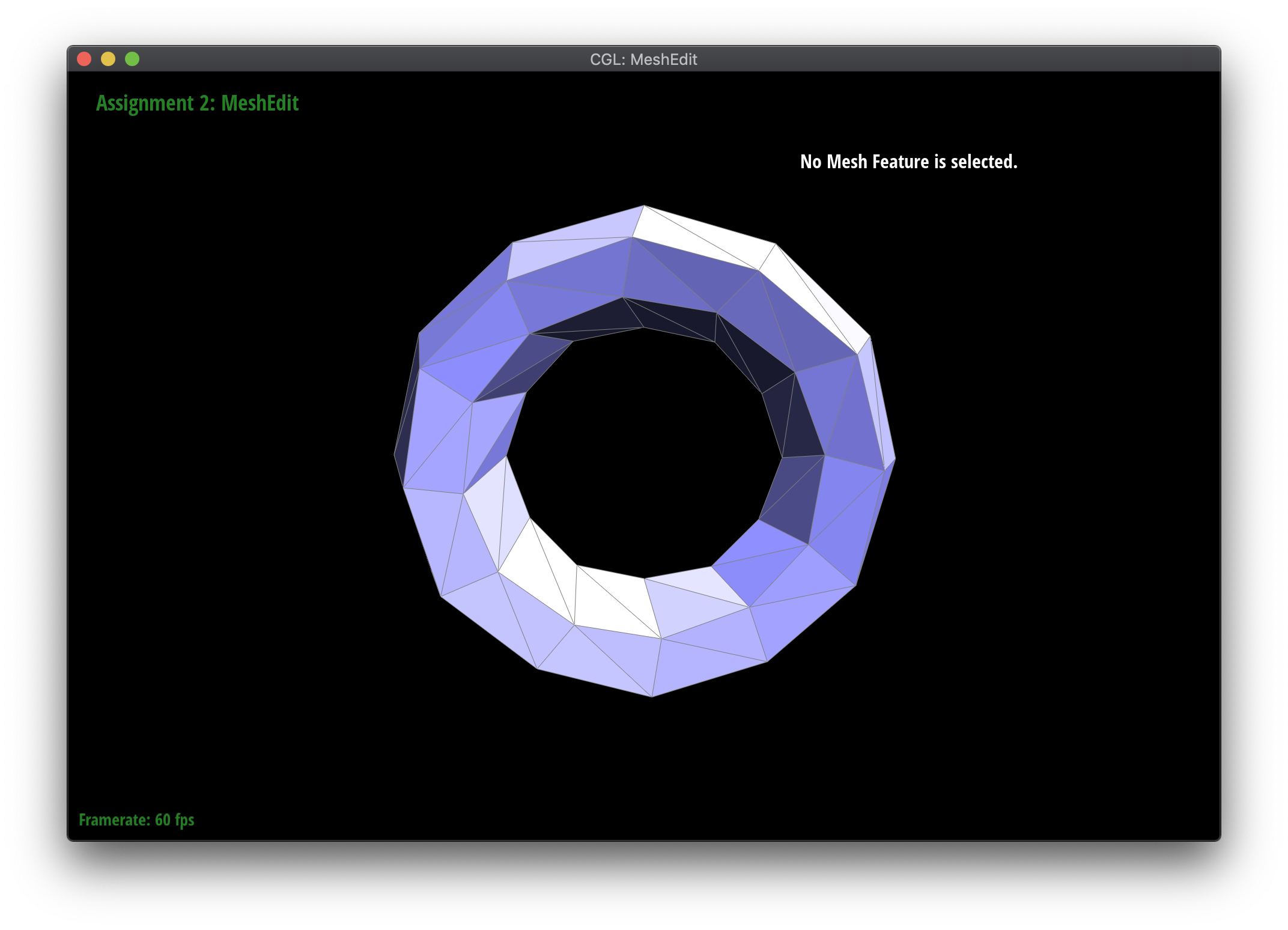
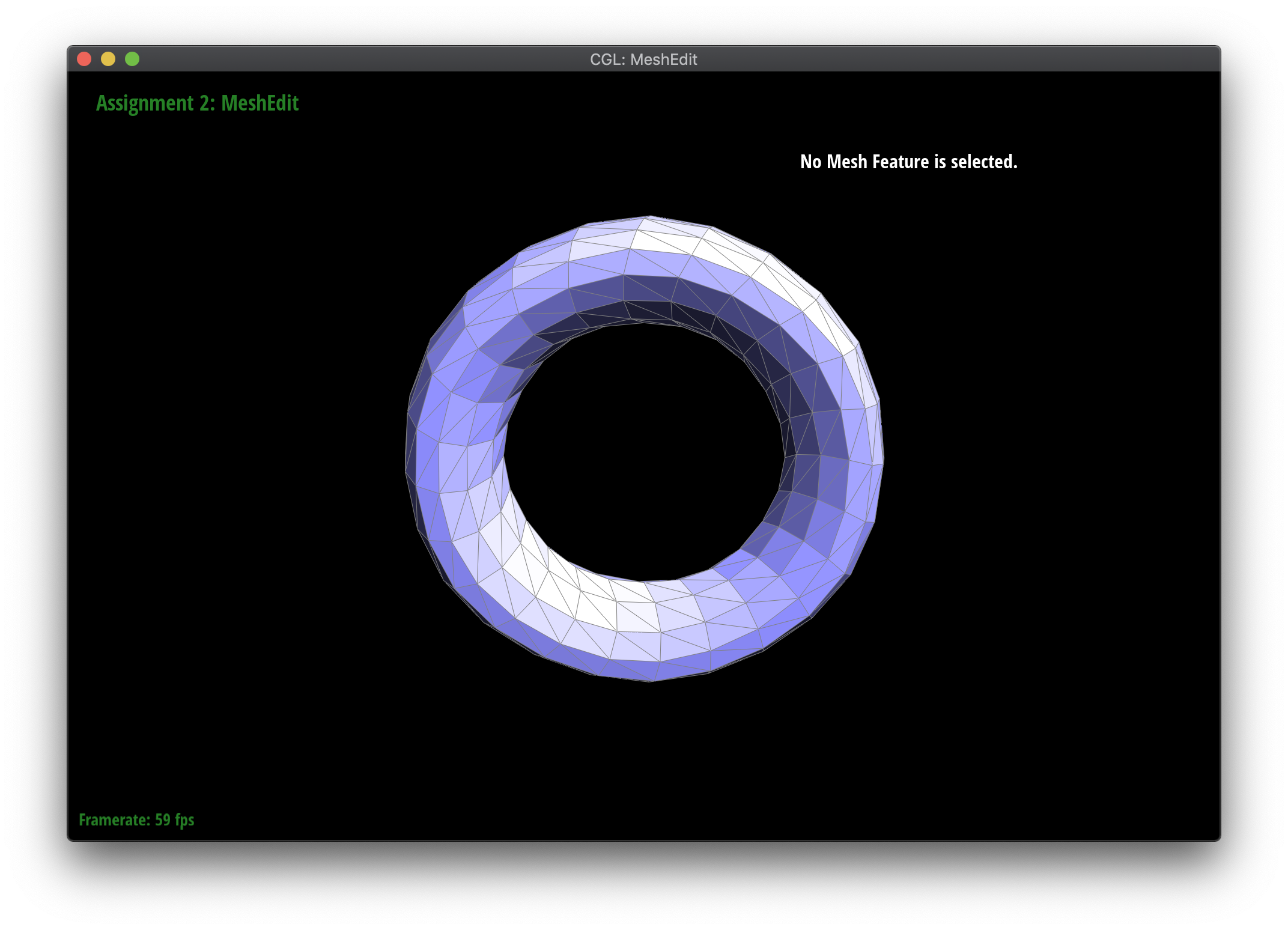
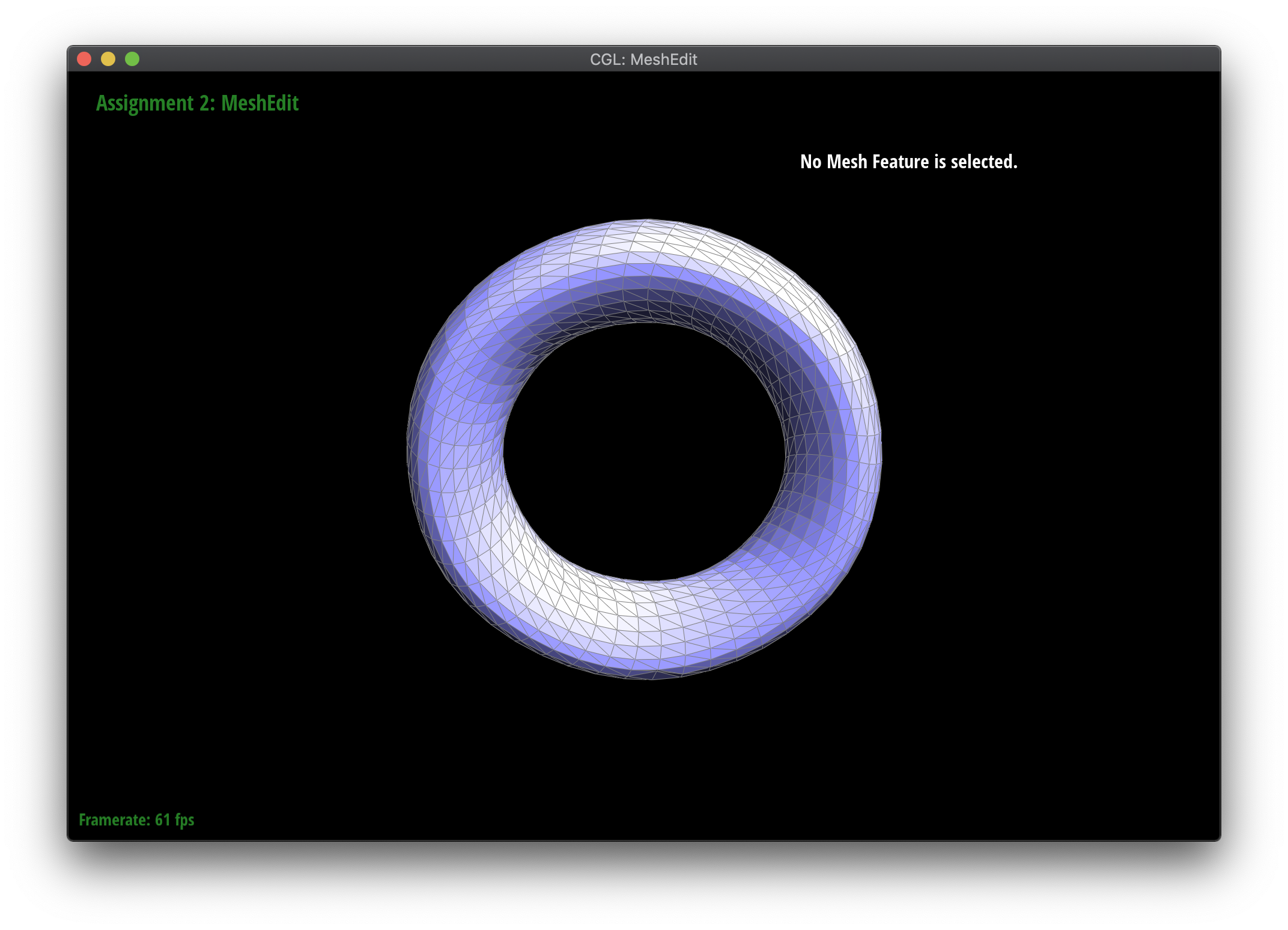
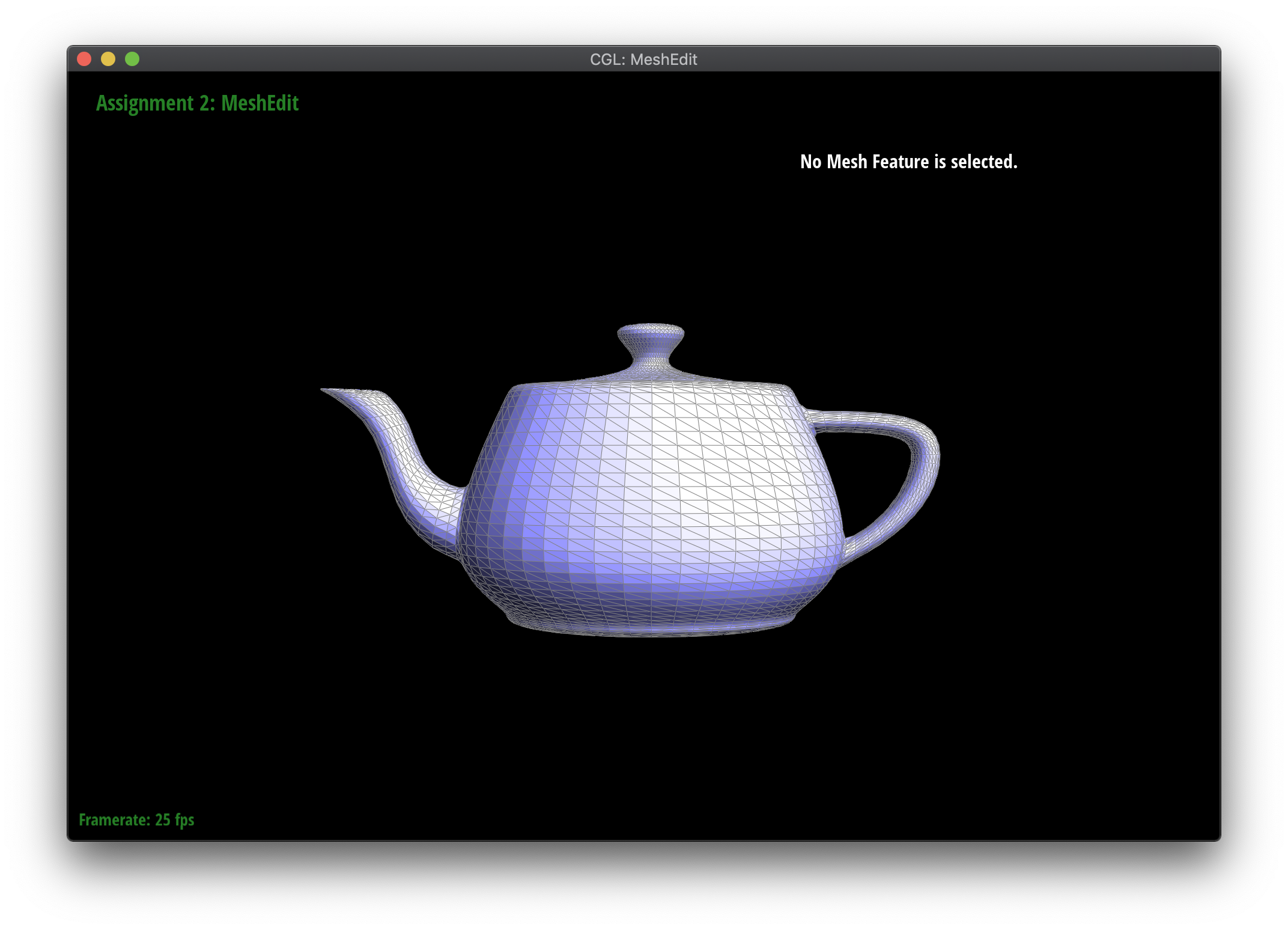
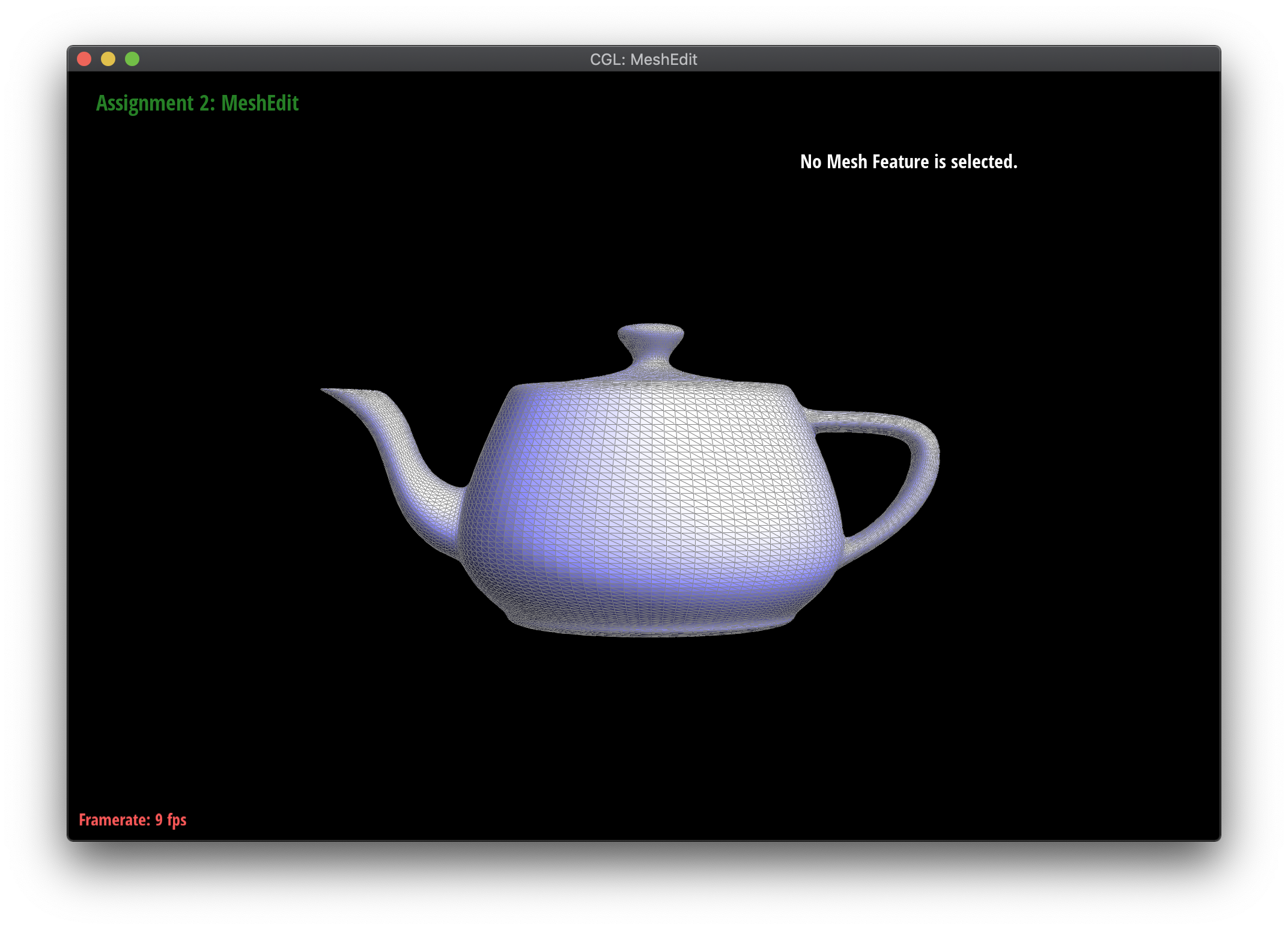
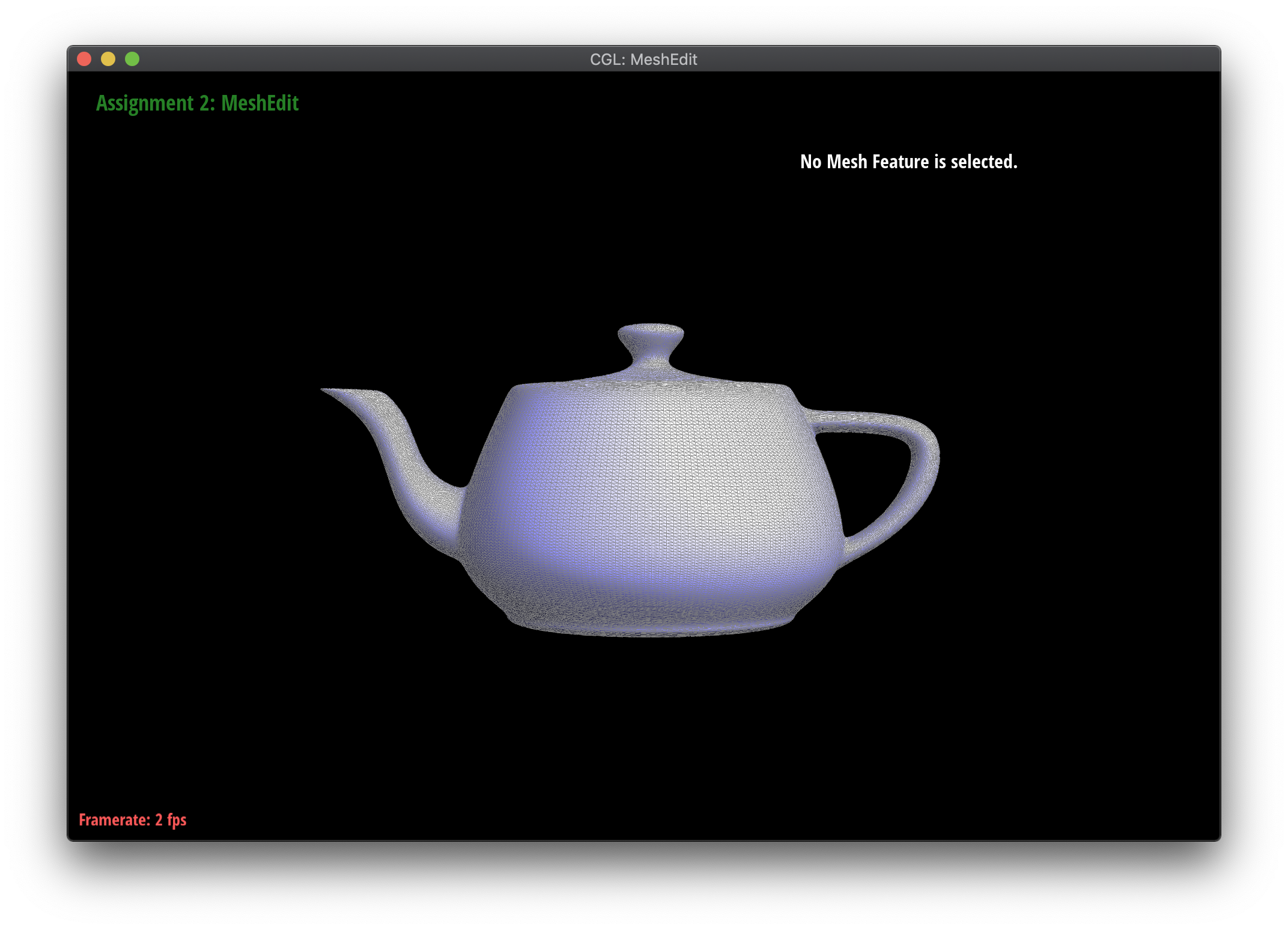
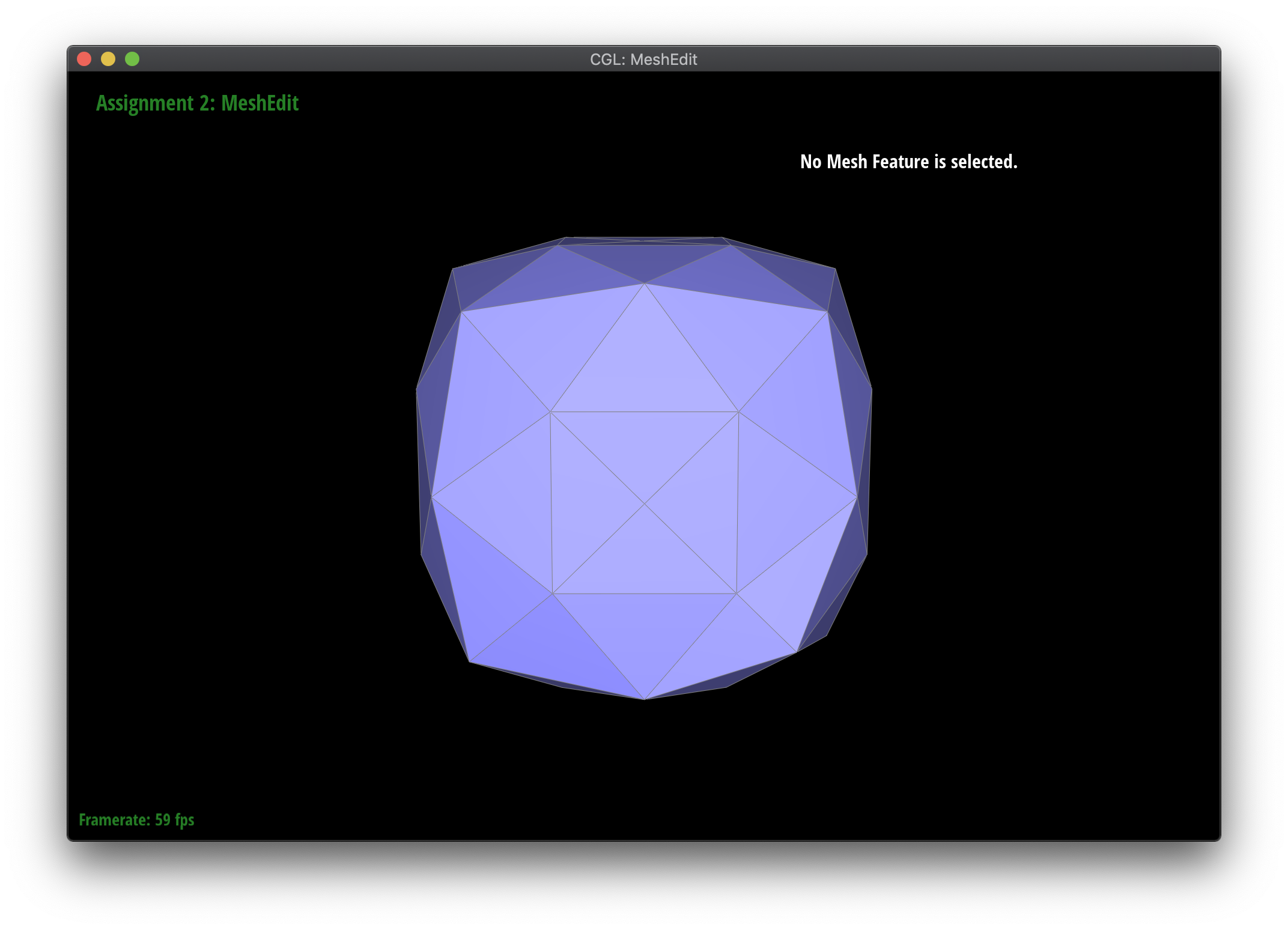
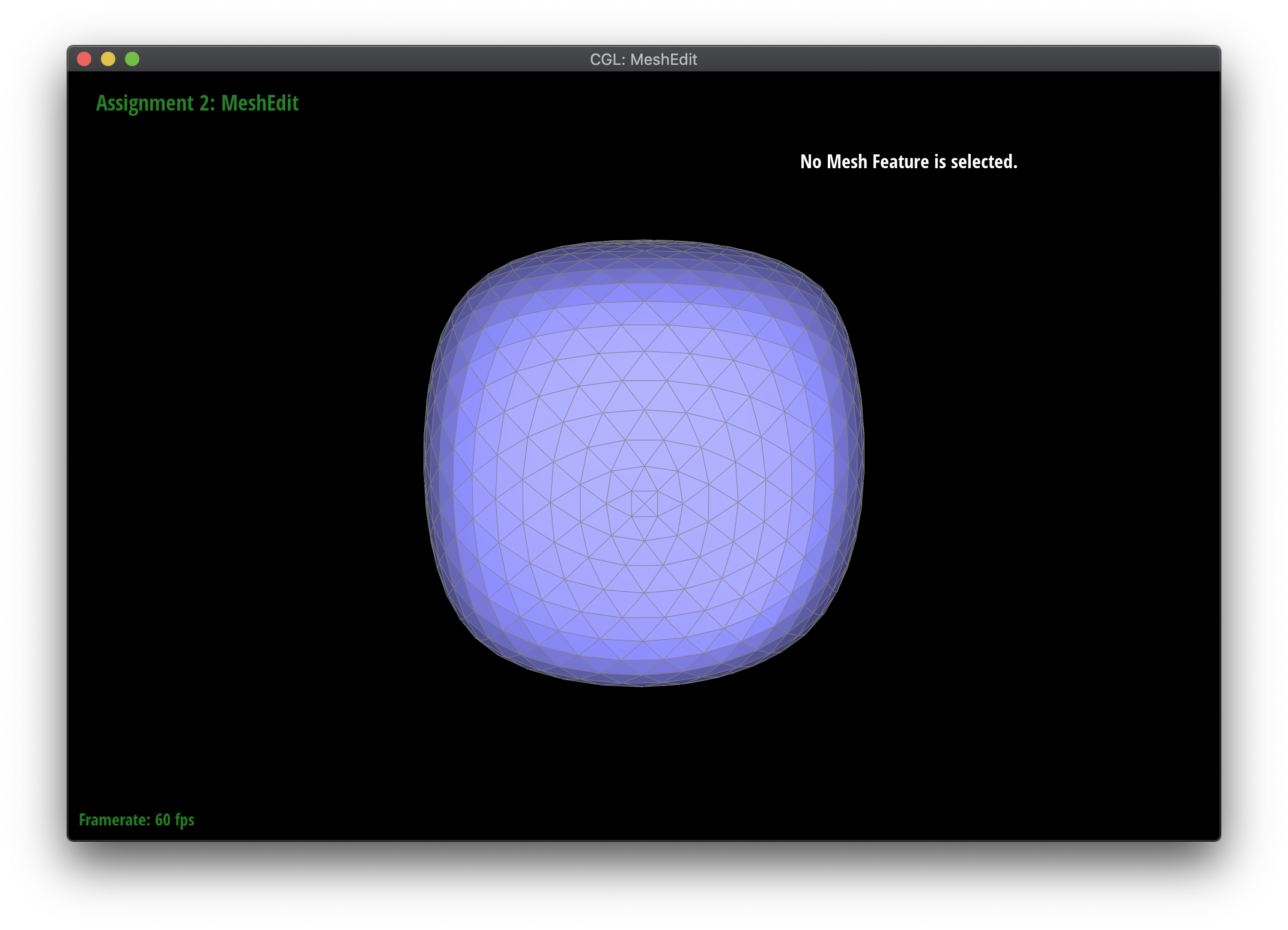
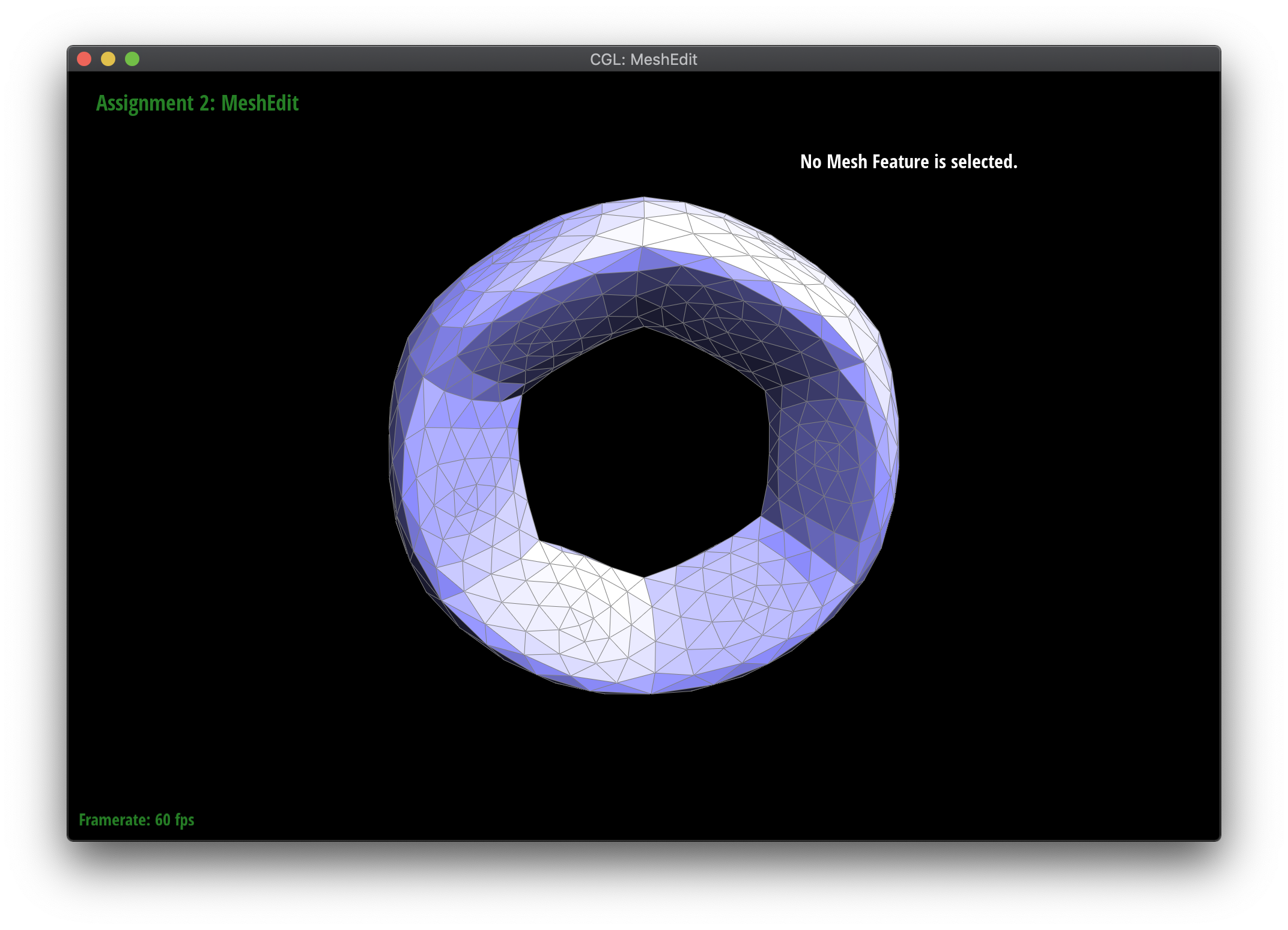
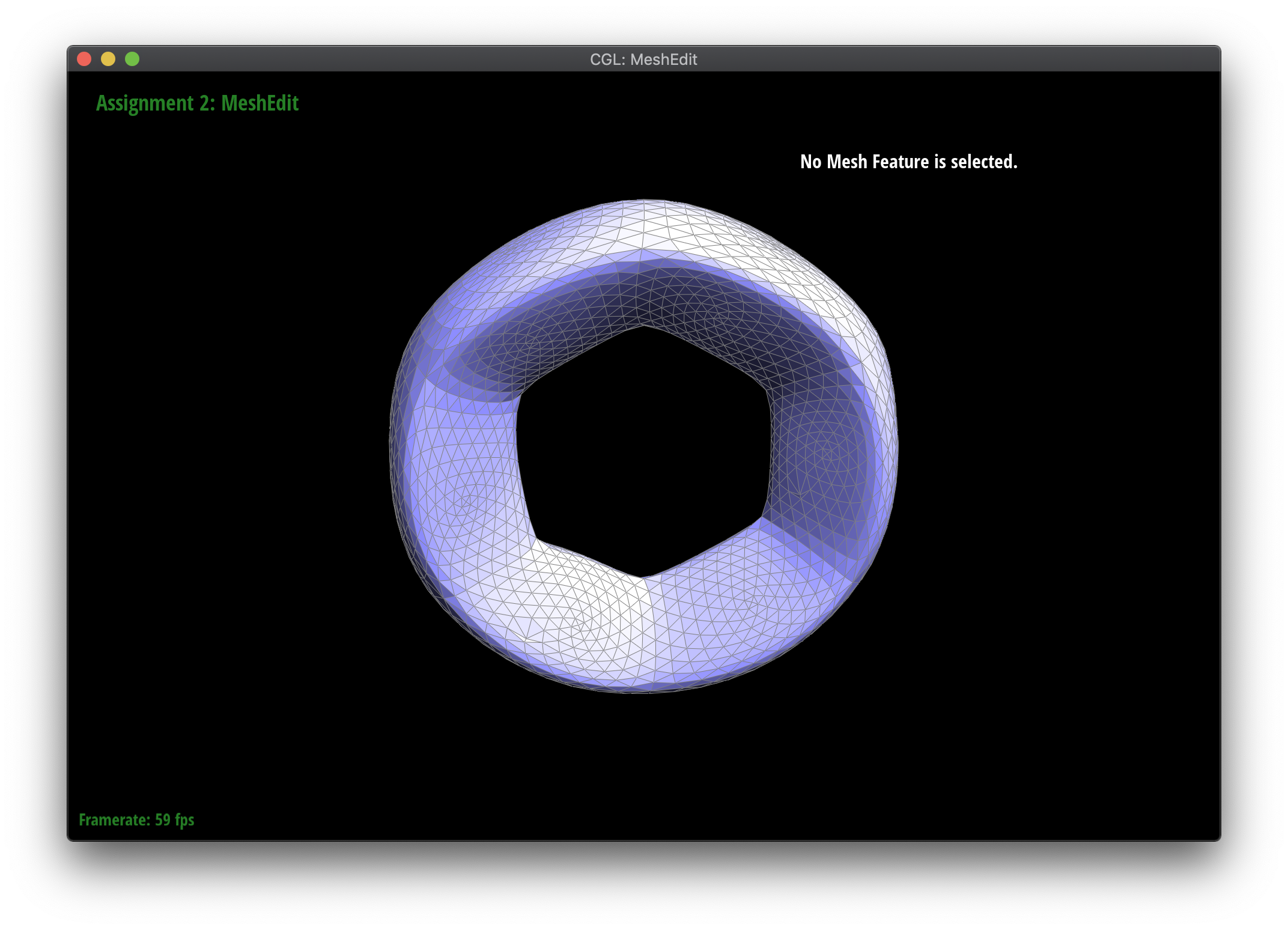
Loop subdivision smooths out sharp edges and creases because the splitting and flipping step prioritizes uniformly shaped triangles and the reweighting step averages positions, acting as a smoothing low pass filter. Especially as seen in the cube and torus below, the sharp angles and edges become smooth and the overall shape is asymmetrical after repeated subdivision.

Meshes at different levels of subdivision.

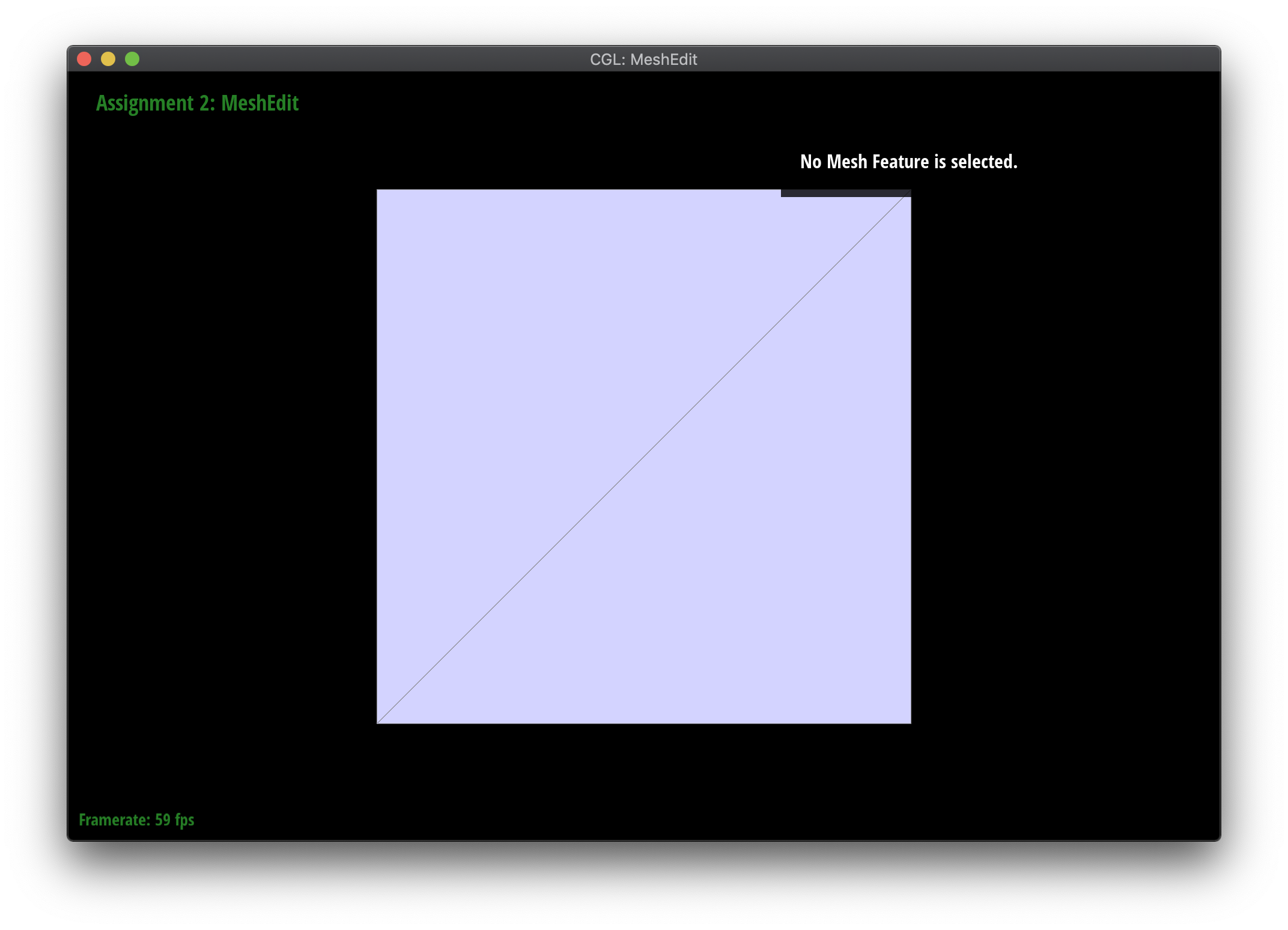
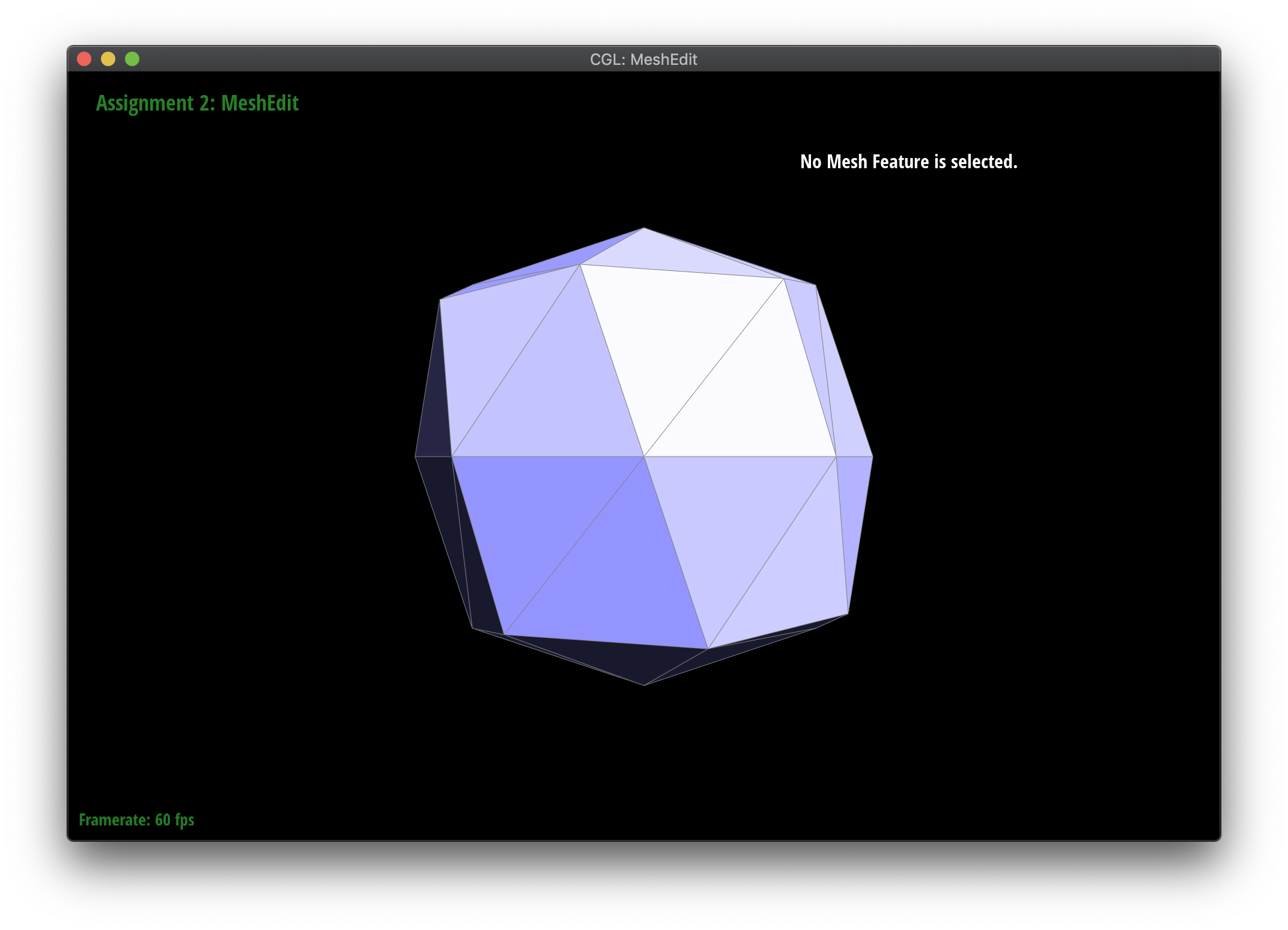
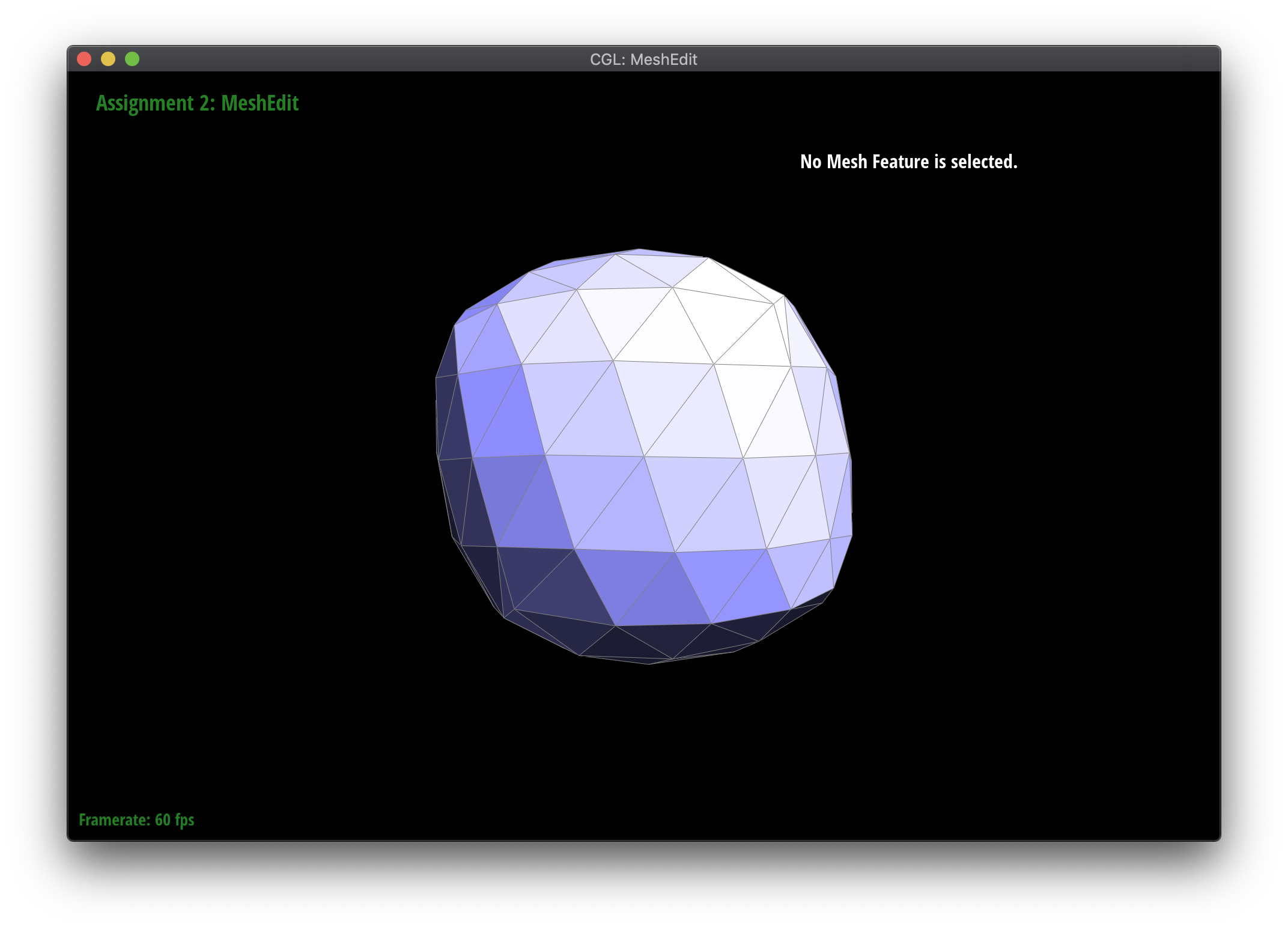
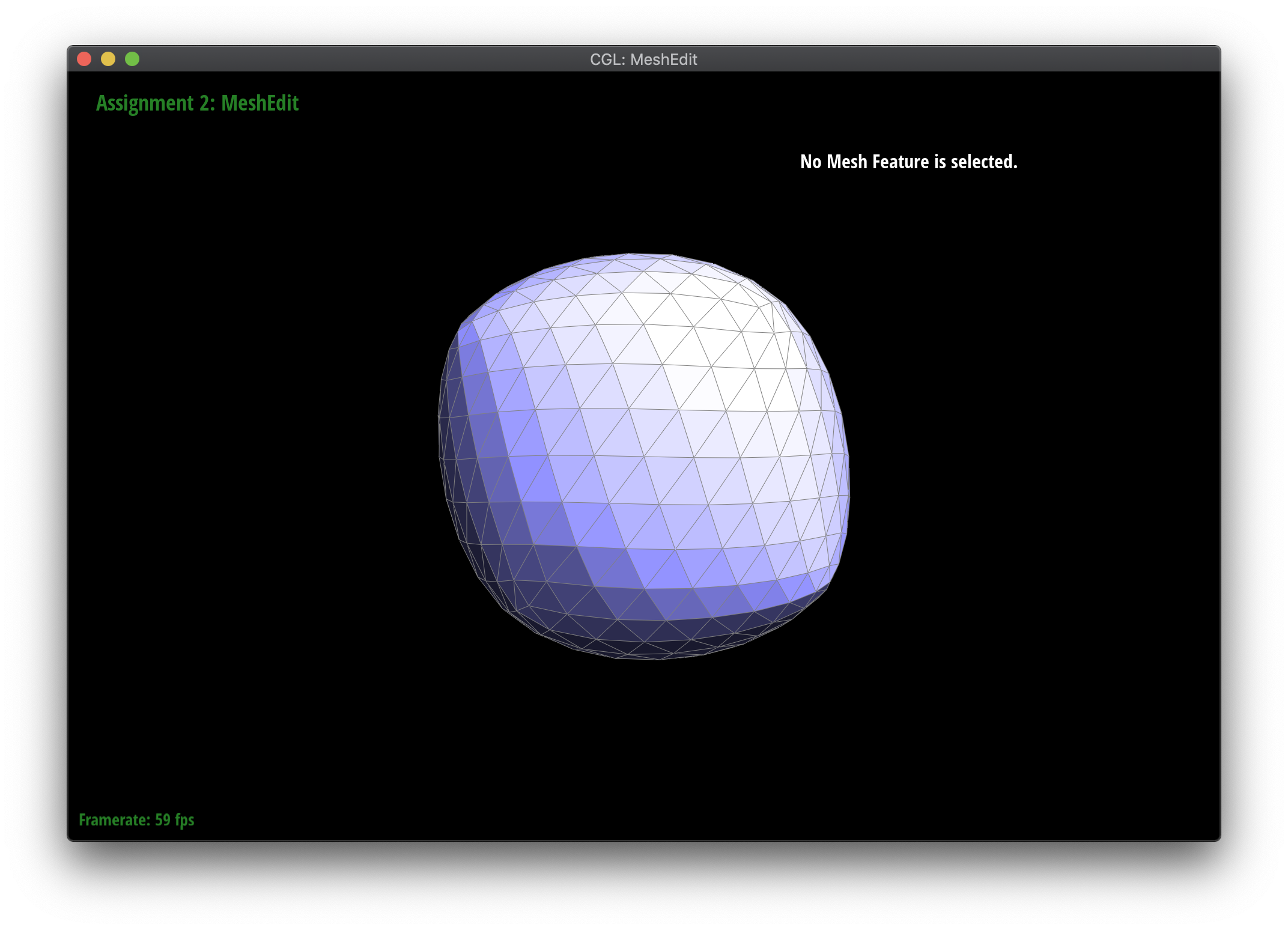
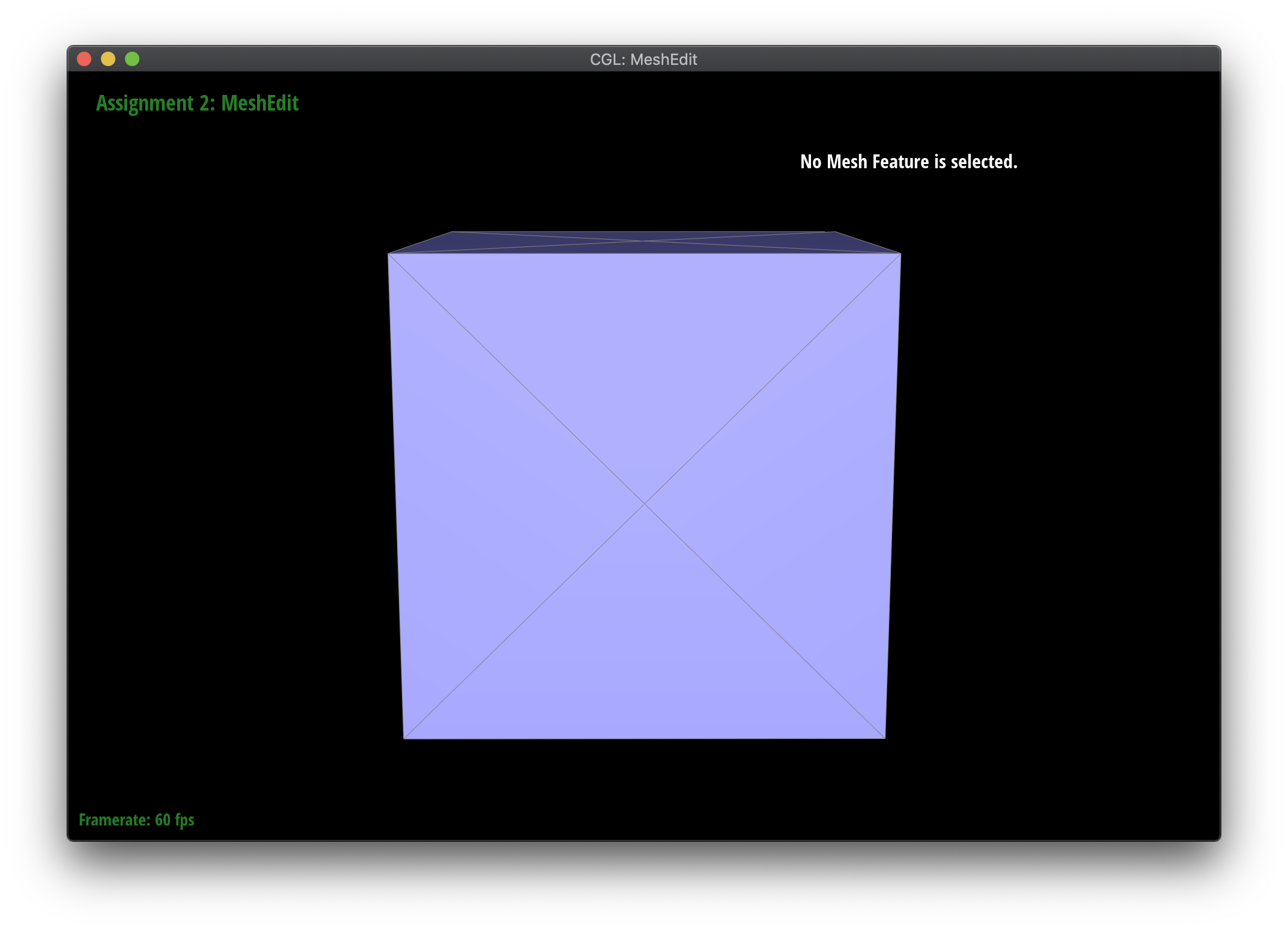
If we want to keep a more symmetrical shape, we can do some preprocessing in the form of presplitting edges. By presplitting the edges within the faces (as opposed to the edges that are the 3D edges of the object), the asymmetrical behavior is alleviated because there will be more subdivision along the faces than the edges not presplit, so the edges are smoothed out slower than the faces.

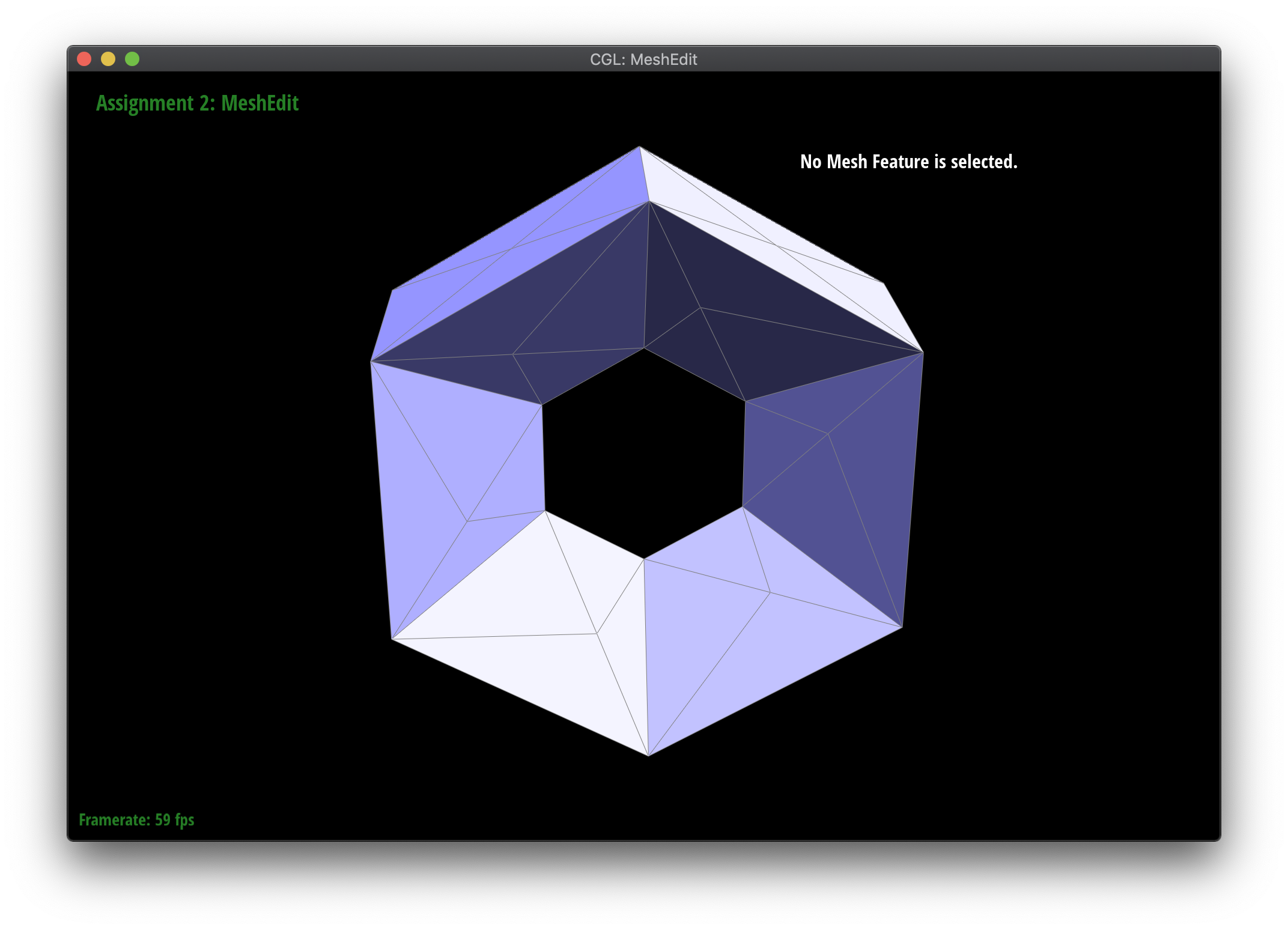
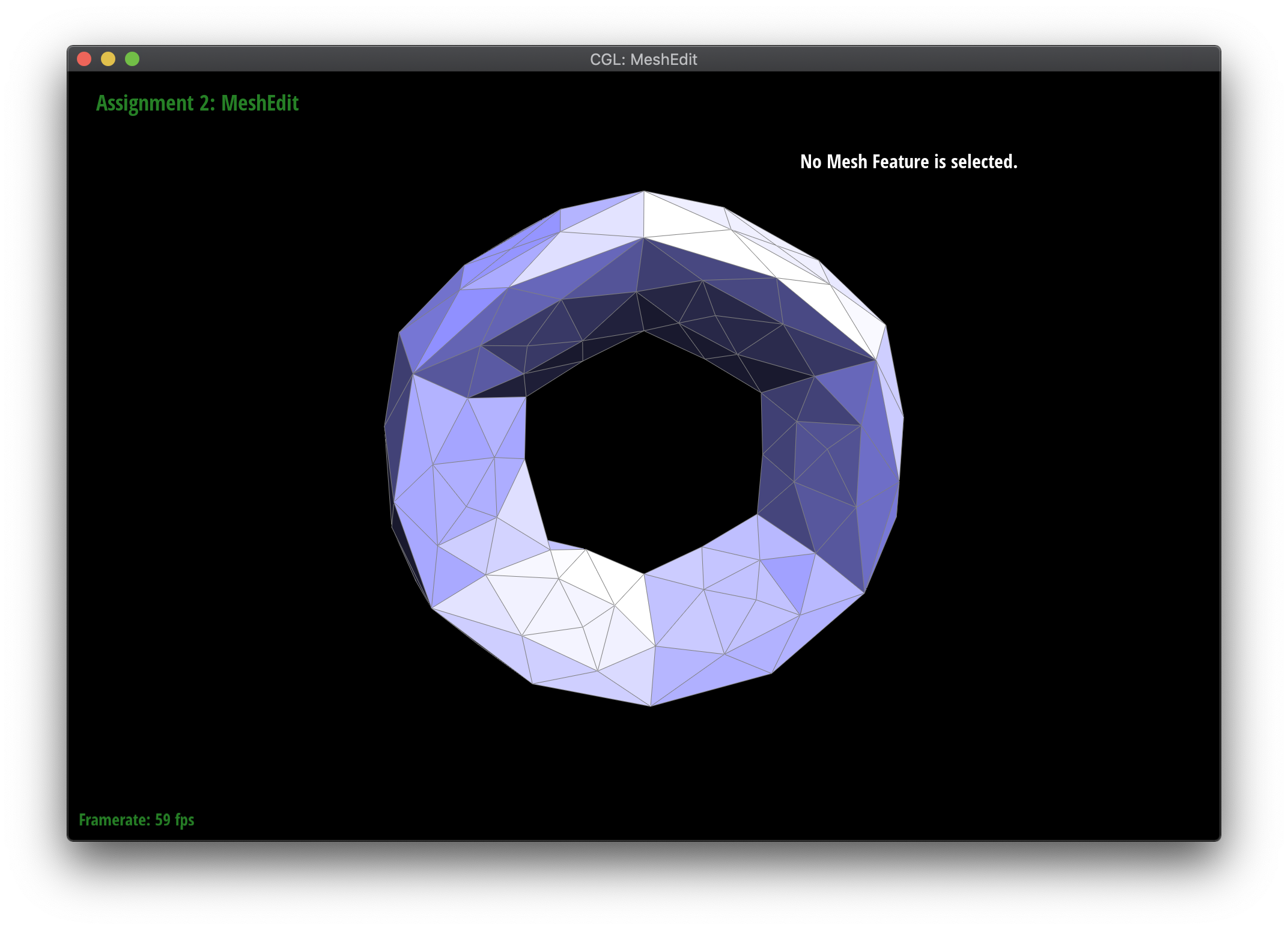
I ran into some visually interesting bugs in the process of debugging this section, shown below. Some of the problems I encountered were using incorrect number types (int versus float), forgetting to set the newPosition attribute correctly, and not flipping only the new edges between new and old vertices.